|
Topics in Quantum Dynamics by A. Jadczyk |
|
| Published in: INFINITE DIMENSIONAL GEOMETRY, NONCOMMUTATIVE GEOMETRY, OPERATOR ALGEBRAS AND FUNDAMENTAL INTERACTIONS Proceedings of the First Caribbean Spring School of Mathematics and Theoretical Physics Saint-François-Guadeloupe 30 May - 13 June 1993 edited by R Coquereaux (CNRS, CPT-Marseille), M Dubois-Violette & P Flad (CNRS, Univ. Paris XI) |  |
Introduction
The Two Kinds of Evolution
In these lectures I will discuss the two kinds of evolution of quantum systems:- CONTINUOUS evolution of closed systems
- STOCHASTIC evolution of open systems.
The Schrödinger Equation
It is rather easy to explain to the mathematician the Dirac equation -
it became already a part of the mathematical folklore. But Dirac's equation
belongs to field theory rather than to
quantum theory. 3 Physicists are being
taught in the course of their education rather early that every attempt at a
sharp localization of a relativistic particle results in creation and
annihilation processes. Sometimes it is phrased as: "there is no relativistic
quantum mechanics - one needs to go directly to Relativistic Quantum Field
Theory". Unfortunately we know of none non-trivial, finite,
relativistic quantum
field theory in four dimensional space-time continuum. Thus we are left
with the mathematics of perturbation theory. Some physicists believe
that the physical ideas of relativistic quantum field theory are sound, that
it is the best theory we ever had, that it is "the exact description of
nature", that
the difficulties we have with it are only temporary, and that they will be
overcomed one day -
the day when bright mathematicians will provide us with new, better, more
powerful tools. Some other say: perturbation theory is more than sufficient
for all practical purposes, no new tools are needed, that is how physics
is - so mathematicians better accept it, digest it, and help the physicists
to make it more rigorous and to understand what it is really about. Still some
other4, a
minority, also believe that it is only a temporary situation, which
one day will be resolved. But the resolution will come
owing to essentially
new physical ideas,
and it will result in a new quantum paradigm, more appealing than the
present one. It should perhaps be not a surprise if, in an appropriate sense,
all
these points of view will turn out to be right. In these lectures we will be
concerned with the well established Schrödinger equation, which is at the
very basis of the current quantum scheme, and with its dissipative
generalization - the Liouville equation.
In these equations we assume that we
know what the time is. Such a knowledge is negated in special
relativity, 5 and this results
in turn in all kinds of troubles that we are facing since the birth of
Einstein's relativity till this day.
6
The Schrödinger equation is more
difficult than the Dirac one, and this for two reasons:
first, it lives on the
background of Galilean relativity - which have to deal with much more
intricate geometric structures than Einstein relativity. 7 Second,
Schrödinger's equation is about Quantum Mechanics and we have to take
care about probabilistic interpretation, observables, states
etc. - which is possible for Schrödinger equation but faces
problems in the first-quantized Dirac theory.
Let me first make a general comment about Quantum Theory. There are physicists
who would say: quantum theory is about calculating of Green's Functions
- all numbers of interest can be obtained from these functions and all the other
mathematical constructs usually connected with quantum theory are superfluous
and unnecessary! It is not my intention to depreciate the achievements of Green's
Function Calculators. But for me quantum theory - as any other physical theory
- should be about explaining things that happen outside of us - as long
as such explanations are possible. The situation in Quantum Theory today,
more than 60 years after its birth, is that Quantum Theory explains much less
than we would like to have been explained. To reduce quantum theory to Green's
function calculations is to reduce its explanatory power almost to zero. It may
of course be that in the coming Twenty First Century humanity will unanimously
recognize the fact that `understanding'was a luxury, a luxury of the "primitive
age" that is gone for ever. But I think it is worth while to take a chance and
to try to understand as much as can be understood in a given situation. Today
we are trying to understand Nature in terms of geometrical pictures and
random processes8 More specifically, in quantum theory, we are
trying to understand in terms of observables, states, complex
Feynman amplitudes etc. In the next chapter, we will show the way that leads
to the Schrödinger Equation using geometrical language as much as
possible. However, we will not use the machinery of geometrical quantization
because it treats time simply as a parameter, and space
as absolute and given once for all. 9On the other hand, geometrical quantization
introduces many advanced tools that are unnecessary for our purposes, while at
the same time it lacks the concepts which are important and necessary.
Before entering the subject let me tell you the distinguishing feature of the
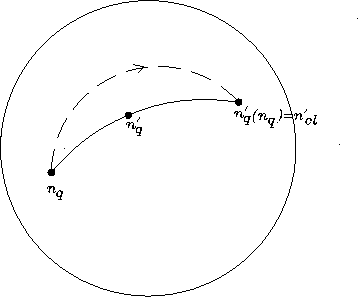
approach that I am advocating, and that will be sketched below in Ch. 2: one obtains
a fibration of Hilbert spaces ![]() over time. There is a distinguished family of local trivializations, a family
parameterized by
over time. There is a distinguished family of local trivializations, a family
parameterized by
- space-time observer
 gauge.
gauge.
| (1) |
| (2) |
In Quantum Mechanics we have a dual scheme - we use the concepts of observables and states. We often use the word measurement in a mutilated sense of simply pairing an observable
One comment is in place here: to compare the results of actual measurements with predictions of the theory - one needs only real numbers. However experience proved that quantum theory with only-real-numbers is inadequate. So, even if the fundamental role of
Now, it is not always clear what is understood by states and observables. There are several possibilities:
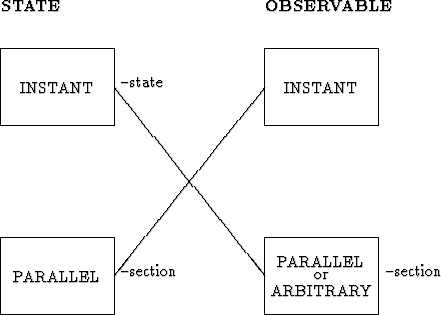 |
As it was already said, it is usual in standard presentations of the quantum
theory to identify the Hilbert spaces ![]() . There are several options there. Either we identify them
according to an observer (+ gauge) or according to the dynamics. If we identify
according to the actual dynamics, then states do not change in time - it is always
the same state-vector, but observables (like position coordinates) do change in
time - we have what is called the Heisenberg picture. If we identify them according
to some background "free" dynamics - we have so called interaction picture.
Or, we can identify Hilbert spaces according to an observer - then observables
do not change in time, but state vector is changing - we get the Schrödinger
picture.
. There are several options there. Either we identify them
according to an observer (+ gauge) or according to the dynamics. If we identify
according to the actual dynamics, then states do not change in time - it is always
the same state-vector, but observables (like position coordinates) do change in
time - we have what is called the Heisenberg picture. If we identify them according
to some background "free" dynamics - we have so called interaction picture.
Or, we can identify Hilbert spaces according to an observer - then observables
do not change in time, but state vector is changing - we get the Schrödinger
picture.
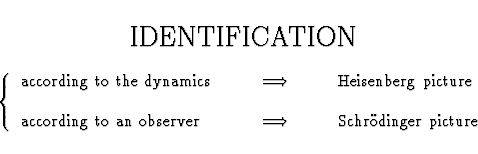
However, there is no reason at all to identify the
Dissipative Dynamics
The Schrödinger equation describes time evolution of pure states of a quantum system, for instance evolution of pure states of a quantum particle, or of a many body system. Even if these states contain only statistical information about most of the physical quantities, the Schrödinger evolution of pure states is continuous and deterministic . Under this evolution Hilbert space vector representing the actual state of the system13 changes continuously with time, and with it there is a continuous evolution of probabilities or potentialities, but nothing happens - the formalism leaves no place for events. Schrödinger equation helps us very little, or nothing at all, to understand how potential becomes real. So, if we aim at understanding of this process of becoming, if we want to describe it by mathematical equations and to simulate it with computers - we must go beyond Schrödinger's dynamics. As it happens, we do not have to go very far - it is sufficient to relax only one (but important) property of Schrödinger's dynamics and to admit that pure states can evolve into mixtures. Instead of Schrödinger equation we have then a so called Liouville equation that describes time evolution of mixed states. It contains Schrödinger equation as a special case.14It was shown in [11] that using the Liouville type of dynamics it is possible to describe coupling between quantum systems and classical degrees of freedom of measurement devices. One can derive also a piecewise deterministic random process that takes place on the manifold of pure states. In this way one obtains a minimal description of "quantum jumps" (or "reduction of wave packets") and accompanying, directly observable jumps of the coupled classical devices. In Ch. 3 simple models of such couplings will be discussed. The interested reader will find more examples in Refs. [8]-[11].15In particular in [11] the most advanced model of this kind, the SQUID-tank model is discussed in details.
Geometry of Schrödinger's Equation
Preliminaries
Galilean General Relativity is a theory of space-time structure, gravitation and electromagnetism based on the assumption of existence of an absolute time function. Many of the cosmological models based on Einstein`s relativity admit also a distinguished time function. Therefore Galilean physics is not evidently wrong. Its predictions must be tested by experiments. Galilean relativity is not that elegant as the one of Einstein. This can be already seen from the group structures: the homogeneous Lorentz group is simple, while the homogeneous Galilei group is a semidirect product of the rotation group and of three commuting boosts. Einstein`s theory of gravitation is based on one metric tensor, while Galilean gravity needs both: space metric and space-time connection. Similarly for quantum mechanics: it is rather straightforward to construct generally covariant wave equations for Einstein`s relativity, while general covariance and geometrical meaning of the Schrödinger equation was causing problems, and it was not discussed in textbooks. In the following sections we will present a brief overview of some of these problems.Galilean General Relativity
Let us discuss briefly geometrical data that are needed for building up generally covariant Schrödinger's equation. More details can be found in Ref. [21].16Our space-time will be a refined version of that of Galilei and of Newton, i.e. space-time with absolute simultaneouity. Four dimensional space-time
Coordinate transformations between any two adapted coordinate systems are of the form:
We will denote by
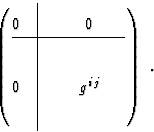
where
We assume a torsion-free connection in
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
The Bundle of Galilei Frames
A basis| (8) |
| (9) |
The Bundle of Velocities
The homogeneous Galilei group| (10) |
| (11) |
We will denote by
The Presymplectic Form
The connection| (12) |
| (13) |
| (14) |
![\begin{displaymath}
\begin{array}{r}
\Omega = g_{lm} \left[ dy^{l}_{0} \wedge
\t...
...mma^{l}_{00}
\right)
dx^{0}\wedge\theta^{m}
\right]
\end{array}\end{displaymath}](img88.gif) |
(15) |
- (i)
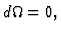
- (ii)
-
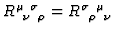 where
where
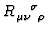 is the curvature
tensor of
is the curvature
tensor of 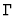 and
and 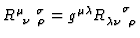
- (iii)
-
![$\partial_{[ \mu} \Phi_{\nu\sigma]}=0 $](img93.gif) . 18
. 18
Quantum Bundle and Quantum Connection
Let ![]() be a principal
be a principal ![]() bundle over
bundle over ![]() and let
and let ![]() be its pullback to
be its pullback to ![]() . We denote by
. We denote by ![]() and
and ![]() the associated Hermitian line bundles corresponding to
the natural action of
the associated Hermitian line bundles corresponding to
the natural action of ![]() on
on ![]() . There is a special class of principal connections on
. There is a special class of principal connections on
![]() , namely those whose connection forms vanish on vectors
tangent to the fibers of
, namely those whose connection forms vanish on vectors
tangent to the fibers of ![]() . As has been discussed in [29] specifying such a connection on
. As has been discussed in [29] specifying such a connection on
![]() is equivalent to specifying a system of connections
on
is equivalent to specifying a system of connections
on ![]() parameterized by the points in the fibers of
parameterized by the points in the fibers of ![]() . Following the terminology of [29] we call such a connection
universal.19The fundamental assumption that leads to the
Schrödinger equations reads as follows:
. Following the terminology of [29] we call such a connection
universal.19The fundamental assumption that leads to the
Schrödinger equations reads as follows:
Quantization Assumption: There exists a universal connection ![]()
![]() whose curvature is
whose curvature is ![]() .20
.20
We call such an ![]() a quantum connection. >From the explicit form of
a quantum connection. >From the explicit form of ![]() one can easily deduce that
one can easily deduce that ![]() is necessarily of the form
is necessarily of the form
where
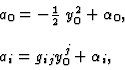
and
Schrödinger's Equation and Schrödinger's Bundle
As it is shown in [21], there exists a natural ![]() -invariant metric on
-invariant metric on ![]() of signature
of signature ![]() . Explicitly
. Explicitly
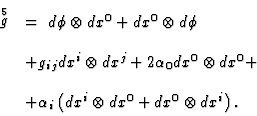
Using this metric we can build out a natural Lagrangian for equivariant functions
More precisely, the construction leading to the generally covariant Schrödinger-Pauli
equation for a charged spin ![]() particle in external gravitational and electromagnetic field can
be described as follows.
particle in external gravitational and electromagnetic field can
be described as follows.
The contravariant metric 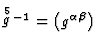 ,
, ![]() ,
,
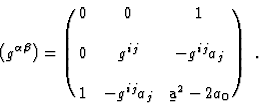 |
(16) |
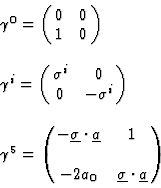 |
(17) |
| (18) |
We finish this section with pointing to the Ref. [21], where Schrödinger's quantization
is discussed in details and where a probabilistic interpretation of generally
covariant Schrödinger equation is given using the bundle ![]() of Hilbert spaces. The parallel transport induced by the
quantum connection is shown in [21] to be directly related to Feynman
amplitudes.
of Hilbert spaces. The parallel transport induced by the
quantum connection is shown in [21] to be directly related to Feynman
amplitudes.
Coupled Quantum and Classical Systems
Preliminaries
Replacing Schrödinger's evolution, which governs the dynamics of pure states, by an equation of the Liouville type, that describes time evolution of mixed states, is a necessary step - but it does not suffice for modeling of real world events. One must take, to this end, two further steps. First of all we should admit that in our reasoning, our communication, our description of facts - we are using classical logic. Thus somewhere in the final step of transmission of information from quantum systems to macroscopic recording devices and further, to our senses and minds, a translation between quantum and classical should take place. That such a translation is necessary is evident also when we consider the opposite direction: to test a physical theory we perform controlled experiments. But some of the controls are always of classical nature - they are external parameters with concrete numerical values. So, we need to consider systems with both quantum and classical degrees of freedom, and we need evolution equations that enable communication in both directions, i.e. :- flow of information from quantum to classical
and - control of quantum states and processes by classical parameters .
Completely Positive Maps
We begin with a brief recall of relevant mathematical concepts. Let Quantum theory gives us a powerful formal language and statistical algorithms
for describing general physical systems. Physical quantities are coded
there by Hermitian elements of a ![]() -algebra
-algebra ![]() of observables, while information about their values
(quantum algorithms deal, in general, only with statistical information) is coded
in states of
of observables, while information about their values
(quantum algorithms deal, in general, only with statistical information) is coded
in states of ![]() . Pure states correspond to a maximal possible information.
For each state
. Pure states correspond to a maximal possible information.
For each state ![]() and for each
and for each ![]() the (real) number
the (real) number ![]() is interpreted as expectation value of observable
is interpreted as expectation value of observable ![]() in state
in state ![]() while
while
is the quadratic dispersion of
Let ![]() be
be ![]() -algebras. A linear map
-algebras. A linear map ![]() is Hermitian if
is Hermitian if ![]() It is positive iff
It is positive iff ![]()
![]() implies
implies ![]() Because Hermitian elements of a
Because Hermitian elements of a ![]() -algebra are differences of two positive ones - each positive
map is automatically Hermitian. Let
-algebra are differences of two positive ones - each positive
map is automatically Hermitian. Let ![]() denote the
denote the ![]() by
by ![]() matrix algebra, and let
matrix algebra, and let ![]() be the algebra of
be the algebra of ![]() matrices with entries from
matrices with entries from ![]() Then
Then ![]() carries a natural structure of a
carries a natural structure of a ![]() -algebra. With respect to this structure a matrix
-algebra. With respect to this structure a matrix ![]() from
from ![]() is positive iff it is a sum of matrices of the form
is positive iff it is a sum of matrices of the form ![]()
![]() If
If ![]() is an algebra of operators on a Hilbert space
is an algebra of operators on a Hilbert space ![]() , then
, then ![]() can be considered as acting on
can be considered as acting on ![]() Positivity of
Positivity of ![]() is then equivalent to
is then equivalent to ![]() or equivalently, to
or equivalently, to ![]() for all
for all ![]()
A positive map ![]() is said to be completely positive or, briefly, CP
iff
is said to be completely positive or, briefly, CP
iff ![]() defined
by
defined
by ![]() , is positive for all
, is positive for all ![]() When written explicitly, complete positivity is equivalent
to
When written explicitly, complete positivity is equivalent
to
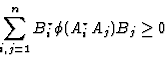 |
(19) |
| (20) |
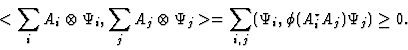 |
(21) |
| (22) |
The space of CP maps from
Dynamical Semigroups
A dynamical semigroup on a ![]() -algebra of operators
-algebra of operators ![]() is a strongly continuous semigroup of CP maps of A into itself.
A semigroup
is a strongly continuous semigroup of CP maps of A into itself.
A semigroup ![]() is norm continuous iff its infinitesimal generator
is norm continuous iff its infinitesimal generator ![]() is bounded as a linear map
is bounded as a linear map ![]() We then have
We then have
| (23) |
Evolution of observables gives rise, by duality, to evolution of positive functionals. One defines
"The dynamics of a finite closed quantum system is conventionally represented
by a one-parameter group of unitary transformations in Hilbert space. This formalism
makes it difficult to describe irreversible processes like the decay of unstable
particles, approach to thermodynamic equilibrium and measurement processes [![]() ]. It seems that the only possibility of introducing an irreversible
behaviour in a finite system is to avoid the unitary time development altogether
by considering non-Hamiltonian systems. "
]. It seems that the only possibility of introducing an irreversible
behaviour in a finite system is to avoid the unitary time development altogether
by considering non-Hamiltonian systems. "
In a recent series of papers [7,8,9,10] Ph. Blanchard and the present
author were forced to introduce dynamical semigroups because of another difficulty,
namely because of impossibility of obtaining a nontrivial Hamiltonian coupling
of classical and quantum degrees of freedom in a system described by an algebra
with a non-trivial centre. We felt that lack of a dynamical understanding of quantum
mechanical probabilistic postulates is more than annoying. We also believed that
the word ''measurement'' instead of being banned, as suggested by J. Bell [5,6], can be perhaps given a precise
and acceptable meaning. We suggested that a measurement process is a coupling
of a quantum and of a classical system, where information about quantum state
is transmitted to the classical recording device by a dynamical semigroup of the
total system . It is instructive to see that such a transfer of information
can not indeed be accomplished by a Hamiltonian or, more generally, by any automorphic
evolution23. To this end consider an algebra ![]() with centre
with centre ![]() Then
Then ![]() describes classical degrees freedom. Let
describes classical degrees freedom. Let ![]() be a state of
be a state of ![]() then
then ![]() denotes its restriction to
denotes its restriction to ![]() Let
Let ![]() be an automorphic evolution of
be an automorphic evolution of ![]() and denote
and denote ![]() Each
Each ![]() is an automorphism of the algebra
is an automorphism of the algebra ![]() and so it leaves its centre invariant:
and so it leaves its centre invariant: ![]() The crucial observation is
that, because of that fact, the restriction
The crucial observation is
that, because of that fact, the restriction ![]() depends only on
depends only on ![]() as the evolution of states of
as the evolution of states of ![]() is dual to the evolution of the observables in
is dual to the evolution of the observables in ![]() This shows that information transfer from the total algebra
This shows that information transfer from the total algebra
![]() to its centre
to its centre ![]() is impossible - unless we use more general, non-automorphic
evolutions.
is impossible - unless we use more general, non-automorphic
evolutions.
>From the above reasoning it may be seen that the Schrödinger picture,
when time evolution is applied to states, is better adapted to a discussion of
information transfer between different systems. The main properties that a dynamical
semigroup ![]() describing time evolution of states should have are:
describing time evolution of states should have are: ![]() should preserve convex combinations, positivity and normalization.
One can demand even more - it is reasonable to demand a special kind of stability:
that it should be always possible to extend the system and its evolution in a
trivial way, by adding extra degrees of freedom that do not couple to our system.24That is exactly what is assured by complete
positivity of the maps
should preserve convex combinations, positivity and normalization.
One can demand even more - it is reasonable to demand a special kind of stability:
that it should be always possible to extend the system and its evolution in a
trivial way, by adding extra degrees of freedom that do not couple to our system.24That is exactly what is assured by complete
positivity of the maps ![]() One could also think that we should require even more, namely
that
One could also think that we should require even more, namely
that ![]() transforms pure states into pure states. But to assume that
would be already too much, as one can prove that then
transforms pure states into pure states. But to assume that
would be already too much, as one can prove that then ![]() must be dual to an automorphic evolution. It appears that
information gain in one respect (i.e. learning about the actual state of the quantum
system) must be accompanied by information loss in another one - as going from
pure states to mixtures implies entropy growth.
must be dual to an automorphic evolution. It appears that
information gain in one respect (i.e. learning about the actual state of the quantum
system) must be accompanied by information loss in another one - as going from
pure states to mixtures implies entropy growth.
We will apply the theory of dynamical semigroup to algebras with a non-trivial
centre. In all our examples we will deal with tensor products of ![]() and an Abelian algebra of functions. The following
theorem by Christensen and Evans [14] generalizes the results of Gorini,
Kossakowski and Sudarshan and of Lindblad to the case of arbitrary
and an Abelian algebra of functions. The following
theorem by Christensen and Evans [14] generalizes the results of Gorini,
Kossakowski and Sudarshan and of Lindblad to the case of arbitrary ![]() -algebra.
-algebra.
| (24) |
| (25) |
| (26) |
Coupling of Classical and Quantum Systems
We consider a model describing a coupling between a quantum and a classical system. To concentrate on main ideas rather than on technical details let us assume that the quantum system is described in an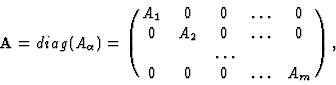
where
Let us consider dynamics. Since the classical system has a discrete set of pure states, there is no non-trivial and continuous time evolution for the classical system that would map pure states into pure states. As for the quantum system, we can have a Hamiltonian dynamics, with the Hamiltonian possibly dependent on time and on the state of the classical system
where
Let us now discuss desired couplings in somewhat vague, but more intuitive, physical terms. We would like to write down a coupling that enables transfer of information from quantum to classical system. There may be many ways of achieving this aim - the subject is new and there is no ready theory that fits. We will see however that a naive description of a coupling works quite well in many cases. The idea is that the simplest coupling associates to a property of the quantum system a transformation of the actual state of the classical system.
Properties are, in quantum theory, represented by projection operators. Sometimes one considers also more general, unsharp or fuzzy properties. They are represented by positive elements of the algebra which are bounded by the unit. A measurement should discriminate between mutually exclusive and exhaustive properties. Thus one usually considers a family of mutually orthogonal projections
As there is no yet a complete, general, theory of dissipative couplings of classical and quantum systems, the best we can do is to show some characteristic examples. It will be done in the following section. For every example a piecewise deterministic random process will be described that takes place on the space of pure states of the total system 28 and which reproduces the Liouville evolution of the total system by averaging over the process. A theory of piecewise deterministic (PD) processes is described in a recent book by M. H. Davis [15]. Processes of that type, but without a non-trivial evolution of the classical system, were discussed also in physical literature - cf. Refs [13,17,18,20]. 29We will consider Liouville equations of the form
where in general
Examples of Classical-Quantum Couplings
The Simplest Coupling
First, we consider only one orthogonal projector| (28) |
![[*]](cross_ref_motif.gif) ) for the density matrix
) for the density matrix 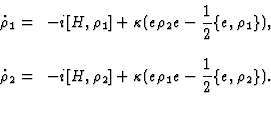 |
(29) |
| (30) |
![[*]](cross_ref_motif.gif) ) describes time evolution of statistical states of the total system.
) describes time evolution of statistical states of the total system. Let us describe now a the PD process associated to this equation. Let
| (31) |
| (32) |
More details about this model illustrating the quantum Zeno effect can be found in Ref. [8].
Simultaneous "Measurement" of Several Noncommuting Observables
Using somewhat pictorial language we can say that in the previous example
each actualization of the property ![]() was causing a flip in the classical system. In the present example,
which is a non-commutative and fuzzy generalization of the model discussed in
[7], we consider
was causing a flip in the classical system. In the present example,
which is a non-commutative and fuzzy generalization of the model discussed in
[7], we consider ![]() in general fuzzy, properties
in general fuzzy, properties ![]() The Hilbert space
The Hilbert space ![]() can be completely arbitrary, for instance
can be completely arbitrary, for instance ![]() -dimensional. We will denote
-dimensional. We will denote ![]() The
The ![]() -s need not be projections, and the different
-s need not be projections, and the different ![]() -s need not to commute. The classical system is assumed to have
-s need not to commute. The classical system is assumed to have ![]() states
states ![]() with
with ![]() thought of as an initial, neutral state. To each actualization of
the property
thought of as an initial, neutral state. To each actualization of
the property ![]() there will be associated a flip between
there will be associated a flip between ![]() and
and ![]() Otherwise the state of the classical system will be unchanged.
To this end we take
Otherwise the state of the classical system will be unchanged.
To this end we take

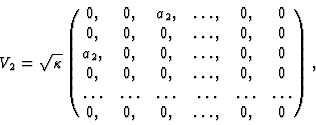
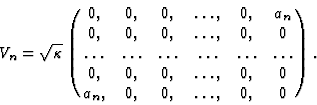
The Liouville equation takes now the following form:
![\begin{displaymath}{\dot \rho_0}= -i[H, \rho_0]+
\kappa \sum_{i=1}^n a_i\rho_i a_i-{\kappa\over 2} \{ a_0^2, \rho_0\} ,
\end{displaymath}](img327.gif) |
(33) |
| (34) |
| (35) |
![\begin{displaymath}{\dot A_0}= i[H, A_0]+
\kappa \sum_{i=1}^n a_iA_i a_i-{\kappa\over 2} \{ a_0^2, A_0\} ,
\end{displaymath}](img330.gif) |
(36) |
| (37) |
| (38) |
| (39) |
| (40) |
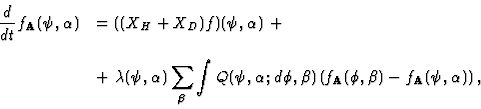 |
(41) |
| (42) |
| (43) |
| (44) |
We describe now PD process associated to the above semigroup. There are
where
If initially the classical system is in a pure state
Then ![]() is the distribution of
is the distribution of ![]() - the first jump time. More precisely,
- the first jump time. More precisely, ![]() is the survival function for the state
is the survival function for the state ![]() :
:
Thus the probability distribution of the jump is
Coupling to All One-Dimensional Projections
In the previous example the coupling between classical and quantum systems involved a finite set of non-commuting observables. In the present one we will go to the extreme - we will use all one-dimensional projections in the coupling. One can naturally discover such a model when looking for a precise answer to the question:
Our model will be formulated for a ![]() -state quantum system. It is rather straightforward to rewrite it for
an arbitrary
-state quantum system. It is rather straightforward to rewrite it for
an arbitrary ![]() -state system, but for
-state system, but for ![]() we can be helped by our visual imagination. Thus we take
we can be helped by our visual imagination. Thus we take ![]() for the Hilbert space of our quantum system. We can
think of it as pure spin
for the Hilbert space of our quantum system. We can
think of it as pure spin ![]() . Pure states of the system form up the manifold
. Pure states of the system form up the manifold ![]() which is isomorphic to the
which is isomorphic to the ![]() -sphere
-sphere ![]() . Let
. Let ![]() ,
, ![]() denote the Pauli
denote the Pauli ![]() -matrices. Then for each
-matrices. Then for each ![]() the operator
the operator ![]() has eigenvalues
has eigenvalues ![]() . We denote by
. We denote by ![]() the projection onto the
the projection onto the ![]() -eigenspace.
-eigenspace.
For the space ![]() of pure states of the classical system we take also
of pure states of the classical system we take also ![]() - a copy of
- a copy of ![]() . Notice that
. Notice that ![]() is a homogeneous space for
is a homogeneous space for ![]() . Let
. Let ![]() be the
be the ![]() invariant measure on
invariant measure on ![]() normalized to
normalized to ![]() . In spherical coordinates we have
. In spherical coordinates we have ![]() . We denote
. We denote ![]() the Hilbert space
of the total system, and by
the Hilbert space
of the total system, and by ![]() its von Neumann algebra of observables. Normal
states of
its von Neumann algebra of observables. Normal
states of ![]() are of the form
are of the form
where
We proceed now to define the coupling of the two systems. There will be two constants:
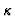 - regulating the time rate of jumps
- regulating the time rate of jumps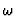 - entering the quantum Hamiltonian
- entering the quantum Hamiltonian
We will use the notation
For each
| (45) |
| (46) |
| (47) |
and therefore
| (48) |
| (49) |
| (50) |
If ![]() , that is if we neglect the Hamiltonian part, then using this
formula we can integrate over
, that is if we neglect the Hamiltonian part, then using this
formula we can integrate over ![]() to get the effective Liouville operator for the quantum state
to get the effective Liouville operator for the quantum state
![]() :
:
| (51) |
| (52) |
Returning back to the case of non-zero ![]() we discuss now the piecewise deterministic random process of
the two pure states
we discuss now the piecewise deterministic random process of
the two pure states ![]() and
and ![]() . To compute it we proceed as in the previous example, with
the only change that now pure states of the quantum and of the classical
system are parameterized by the same set -
. To compute it we proceed as in the previous example, with
the only change that now pure states of the quantum and of the classical
system are parameterized by the same set - ![]() in our case. To keep track of the origin of each parameter we will
use subscripts as in
in our case. To keep track of the origin of each parameter we will
use subscripts as in ![]() and
and ![]() . As in the previous example each observable
. As in the previous example each observable ![]() of the total system determines a function
of the total system determines a function ![]() by
by
The Liouville operator
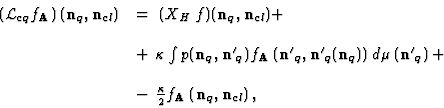 |
(53) |
| (54) |
| (55) |
The PD process on
Acknowledgements: This paper is partially based on a series of publications that were done in a collaboration with Ph. Blanchard and M. Modugno. Thanks are due to the Humboldt Foundation and Italian CNR that made this collaboration possible. The financial support for the present work was provided by the Polish KBN grant No PB 1236 on one hand, and European Community program "PECO" handled by the Centre de Physique Theorique (Marseille Luminy) on the other. Parts of this work have been written while I was visiting the CPT CNRS Marseille. I would like to thank Pierre Chiapetta and all the members of the Lab for their kind hospitality. Thanks are due to the Organizers of the School for invitation and for providing travel support. I would like to express my especially warm thanks to Robert Coquereaux for his constant interest, criticism and many fruitful discussions, and for critical reading of much of this text. Thanks are also due to Philippe Blanchard for reading the paper, many discussions and for continuous, vital and encouraging interaction.
Bibliography
- 1
- Aharonov, Y. and Vaidman, L. : "Measurement of the Schrödinger wave of a single particle", Phys. Lett. A178 (1993), 38-42
- 2
- Arveson, W. B. : "Subalgebras of
 -algebras", Acta Math. 123 (1969), 141-224
-algebras", Acta Math. 123 (1969), 141-224
- 3
- Asorey, M. , Cariñena, J. F. , and Parmio, M. : "Quantum Evolution as a parallel transport", J. Math. Phys. 23 (1982), 1451-1458
- 4
- Barnsley, M. F. : Fractals everywhere, Academic Press, San Diego 1988
- 5
- Bell, J. : "Against measurement", in Sixty-Two Years of Uncertainty. Historical, Philosophical and Physical Inquiries into the Foundations of Quantum Mechanics, Proceedings of a NATO Advanced Study Institute, August 5-15, Erice, Ed. Arthur I. Miller, NATO ASI Series B vol. 226 , Plenum Press, New York 1990
- 6
- Bell, J. : "Towards an exact quantum mechanics", in Themes in Contemporary Physics II. Essays in honor of Julian Schwinger's 70th birthday, Deser, S. , and Finkelstein, R. J. Ed. , World Scientific, Singapore 1989
- 7
- Blanchard, Ph. and Jadczyk, A. : "On the interaction between classical and quantum systems", Phys. Lett. A 175 (1993), 157-164
- 8
- Blanchard, Ph. and Jadczyk, A. : "Strongly coupled quantum and classical systems and Zeno's effect", Phys. Lett. A 183 (1993), 272-276
- 9
- Blanchard, Ph. and Jadczyk, A. : "Classical and quantum intertwine", in Proceedings of the Symposium on Foundations of Modern Physics, Cologne, June 1993, Ed. P. Mittelstaedt, World Scientific (1993)
- 10
- Blanchard, Ph. and Jadczyk, A. : "From quantum probabilities to classical facts", in Advances in Dynamical Systems and Quantum Physics, Capri, May 1993, Ed. R. Figari, World Scientific (1994)
- 11
- Blanchard, Ph. and Jadczyk, A. : "How and When Quantum Phenomena Become Real", to appear in Proc. Third Max Born Symp. "Stochasticity and Quantum Chaos", Sobotka, Eds. Z. Haba et all. , Kluwer Publ.
- 12
- Canarutto, D. , Jadczyk, A. , Modugno, M. : in preparation
- 13
- Carmichael, H. : An open systems approach to quantum optics, Lecture Notes in Physics m 18, Springer Verlag, Berlin 1993
- 14
- Christensen, E. and Evans, D. : "Cohomology of operator algebras and quantum dynamical semigroups", J. London. Math. Soc. 20 (1978), 358-368
- 15
- Davies, E. B. : "Uniqueness of the standard form of the generator of a quantum dynamical semigroup", Rep. Math. Phys. 17 (1980), 249-255
- 16
- Davis, M. H. A. : Markov models and optimization, Monographs on Statistics and Applied Probability, Chapman and Hall, London 1993
- 17
- Dalibard, J. , Castin, Y. and Mølmer K. : "Wave-function approach to dissipative processes in quantum optics", Phys. Rev. Lett. 68 (1992), 580-583
- 18
- Dum, R. , Zoller, P. , and Ritsch, H. : "Monte Carlo simulation of the atomic master equation for spontaneous emission", Phys. Rev. A45 (1992), 4879-4887
- 19
- Duval, C. , Burdet, G. , Künzle, H. P. and Perrin, M. : "Bargmann structures and Newton-Cartan theory", Phys. Rev. D31, 1841-1853
- 20
- Gardiner, C. W. , Parkins, A. S. , and Zoller, P. : "Wave-function stochastic differential equations and quantum-jump simulation methods", Phys. Rev. A46 (1992), 4363-4381
- 21
- Jadczyk, A. and Modugno, M. : Galilei general relativistic quantum mechanics, Preprint, pp. 1-185, Florence 1993
- 22
- Gorini, V. , Kossakowski, A. and Sudarshan, E. C. G. : "Completely positive dynamical semigroups of N-level systems", J. Math. Phys. 17 (1976), 821-825
- 23
- Itzikson, C. and Zuber, J. -B. " Quantum Field Theory, McGraw-Hill Book Co. , New York 1980
- 24
- Künzle, H. P. and Duval, C. : "Dirac Field on Newtonian Space-Time", Ann. Inst. H. Poincaré 41 (1984), 363-384
- 25
- Landsman, N. P. : "Algebraic theory of superselection sectors and the measurement problem in quantum mechanics", Int. J. Mod. Phys. A6 (1991), 5349-5371
- 26
- Lasota, A. and Mackey, M. C.: Chaos, Fractals and Noise. Stochastic Aspects of Dynamics, Springer Verlag, New York 1994
- 27
- Lindblad, G. : "On the Generators of Quantum Mechanical Semigroups", Comm. Math. Phys. 48 (1976), 119-130
- 28
- Lüders, G. : "Über die Zustandsänderung durch den Messprozzess", Annalen der Physik 8 (1951), 322-328
- 29
- Modugno, M. : "Systems of vector valued forms on a fibred manifold and applications to gauge theories", Lect. Notes in Math. 1251, Springer Verlag, 1987
- 30
- von Neumann, J. : Mathematical Foundations of Quantum Mechanics, Princeton Univ. Press, Princeton 1955
- 31
- Ozawa, M.: "Cat Paradox for
 -Dynamical Systems", Progr. Theor. Phys. 88
(1992), 1051-1064
-Dynamical Systems", Progr. Theor. Phys. 88
(1992), 1051-1064
- 32
- Parthasarathy, K. R. : An Introduction to Quantum Stochastic Calculus, Birkhäuser Verlag, Basel 1992
- 33
- Sniatycki, J. : Geometric Quantization and Quantum Mechanics, Springer
Verlag, New York 1980
About this document ...
Topics in Quantum DynamicsThis document was generated using the LaTeX2HTML translator Version 99.1 release (March 30, 1999)
Copyright © 1993, 1994, 1995, 1996, Nikos
Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross
Moore, Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -local_icons 9406204.tex
Footnotes
- ... isolated1
- Emphasized style will be used in these notes for concepts that are important, but will not be explained. Sometimes explanation would need too much space, but sometimes because these are either primitive or meta-language notions.
- ... observable.2
- Lüders [28] noticed that this formulation is ambiguous in case of degenerate eigenvalues, and generalized it to cover also this situation.
- ... theory.3
- In these lectures, "quantum theory" usually means "quantum mechanics", although much of the concepts that we discuss are applicable also to systems with infinite number of degrees of freedom and in particular to quantum field theory.
- ... other4
- Including the author of these notes.
- ... relativity,5
- There exists however so called "relativistic Fock-Schwinger proper time formalism" [23, Ch. 2-5-4] where one writes Schrödinger equation with Hamiltonian replaced by "super-Hamiltonian, and time replaced by "proper time"
- ... day.6
- One could try to "explain" time by saying that there is a preferred time direction selected by the choice of a thermal state of the universe. But that is of no help at all, until we are told how it happens that a particular thermal state is being achieved.
- ... relativity.7
- In group theoretical terms: the proper Lorentz group is simple, while the proper Galilei group is not.
- ... processes8
- The paradigm may however change in no so distant future - we may soon try to understand the Universe as a computing machine, with geometry replaced by geometry of connections, and randomness replaced by a variant of algorithmic complexity.
- ... all.9
- Cf. e. g. Ref. [33, Ch. 9].
- .... 10
- A similar idea was mentioned in [3]. For a detailed description of all the constructions - see the forthcoming book [21]
- ... confusion.11
- Notable exceptions can be found in publications from the Genevé school of Jauch and Piron.
- ... etc.12
- Quaternionic structures, on the other hand, can be always understood as complex ones with an extra structure - they are unnecessary.
- ... system13
- Some physicists deny "objectivity" of quantum states - they would say that Hilbert space vectors describe not states of the system, but states of knowledge or information about the system. In a recent series of papers (see [1] and references therein) Aharonov and Vaidman [1] attempt to justify objectivity of quantum states. Unfortunately their arguments contain a loophole.
- ... case.14
- It should be noted, however, that Schrödinger equation describes evolution of state vectors. and thus contains direct information about phases. This information is absent in the Liouville equation, and its restoration (e. g. as it is with the Berry phase) may sometimes create a non-trivial task.
- ...bla5.15
- Cf. also the recent (June 1994) paper "Particle Tracks, Events and Quantum Theory", by the author.
- ...jamo.16
- The reader may also consult [19], where a different approach, using dimensional reduction along a null Killing vector, is discussed.
- .... 17
- Some of these assumptions are superfluous as they would follow anyhow from
the assumption
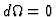 in the next paragraph.
in the next paragraph.
- .... 18
- Notice that because
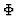 is not a tensor, the last condition need not be, a priori, generally
covariant.
is not a tensor, the last condition need not be, a priori, generally
covariant.
- ... universal.19
- i.e. universal for the system of connections.
- ...
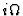 .20
.20
- We choose the physical units in such a way that the Planck constant
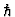 and mass of the quantum particle
and mass of the quantum particle 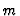 are equal to 1.
are equal to 1.
- ... factor.21
- For an alternative detailed derivation see [12]
- ... 22
- Our point is that "measurement" is an undefined concept in standard quantum theory, and that the probabilistic interpretation must be, because of that, brought from outside. What we propose is to define measurement as a CP semigroup coupling between a classical and a quantum system and to derive the probabilistic interpretation of the quantum theory from that of the classical one.
- ... evolution23
- For a discussion of this fact in a broader context of algebraic theory of superselection sectors - cf. Landsman [25, Sec. 4. 4]. Cf. also the no-go result by Ozawa [31]
- ... system.24
- That requirement is also necessary to guarantee physical consistency of the whole framework, as we always neglect some degrees of freedom as either irrelevant or yet unknown to us.
- ... extremal25
- It should be noticed, however, that splitting of
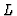 into
into 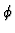 and
and 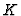 is, in general, not unique - cf. e. g. Refs [15] and [32, Ch. III. 29-30].
is, in general, not unique - cf. e. g. Refs [15] and [32, Ch. III. 29-30].
- ... 26
- It is useful to have the algebra
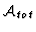 represented in such a form, as it enables us to apply
the theorem of Christensen-Evans.
represented in such a form, as it enables us to apply
the theorem of Christensen-Evans.
- ... 27
- One can easily imagine a more general situation when tracing over the classical
system will not be meaningful. This can happen if we deal with several phases
of the quantum system, parameterized by the classical parameter
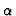 . It may then happen that the total algebra is not the tensor
product algebra. For instance, instead of one Hilbert space
. It may then happen that the total algebra is not the tensor
product algebra. For instance, instead of one Hilbert space 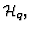 we may have, for each value of
we may have, for each value of 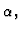 a Hilbert space
a Hilbert space 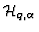 of dimension
of dimension 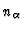 .
.
- ... system28
- One may wonder what does that mean mathematically, as the space of pure states
of a
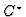 algebra is, from measure-theoretical point of view, a rather
unpleasant object. The answer is that the only measures on the space of pure states
of the quantum algebra will be the Dirac measures.
algebra is, from measure-theoretical point of view, a rather
unpleasant object. The answer is that the only measures on the space of pure states
of the quantum algebra will be the Dirac measures.
- ...car,dal,dum,gar. 29
- Thanks are due to N. Gisin for pointing out these references.
- ... transformations30
- Or, more precisely, as Frobenius-Perron operators. Cf. Ref.[26] for definition and examples of Frobenius-Perron and dual to them Koopman operators.
- .... 31
- This sequence of transformation on the space of pure states of the quantum system can be thought of as a nonlinear version of Barnsley's Iterated Function System (cf. e. g. [4]
- ... details.32
- I do not think that they found the answer, as their arguments are circular, and they seem to be well aware of this circularity.
- ... formula:33
- The formula is easily established for
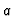 of the form
of the form 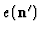 , and then extended to arbitrary operators by linearity.
, and then extended to arbitrary operators by linearity.
.