Abstract

Departing from classical concepts of ergodic theory, formulated in terms of probability densities, measures describing the mixing behavior and the loss of information in quantum open systems are proposed. As application we discuss the chaotic outcomes of continuous measurement processes in the EEQT framework. Simultaneous measurement of four noncommuting spin components is shown to lead to a chaotic jumps on the quantum spin sphere and to generate specific fractal images of a nonlinear iterated function system.

1. Introduction

In the past two decades the study of chaotic dynamical systems has attracted attention of many physicists. Roughly speaking, a system is said to be chaotic if orbits of the motion are in some sense irregularly distributed. One of the most useful measures of this irregularity is the Kolmogorov-Sinai entropy. Another important quantity relevant to control the chaotic behavior is the Lyapunov exponents, which measure the exponential instability of almost all orbits with respect to the change of initial conditions. It turns this instability leads to the loss of memory of initial conditions, decay of correlations and approach to statistical equilibrium.

It is believed that also quantum systems have different qualitative properties depending on whether the corresponding classical systems are integrable or chaotic [1]. For example, they reveal significant differences in the character of their wave functions or the distribution of their energy levels [2]. Also the numerical analysis of some finite quantum systems shows quantitative differences in regular and chaotic regime [3]. It is obvious that on the quantum level the distinction between chaotic and quasiperiodic behavior must be blurred, nevertheless some relative measure of the degree of chaos should exist. There have been many attempts to find fingerprints of chaotic behavior in quantum dynamical systems. The most natural one is based on the correspondence principle, which states that a quantum system is chaotic if its classical limit is chaotic. However, it can only indicate some features of chaotic behavior but cannot serve as a precise definition. As was pointed out by van Kampen [4] such notions like ergodicity or mixing need a limit t --> oo while the correspondence principle refers to h --> 0, and these two limits do not commute. Moreover, an example of a chaotic quantum phenomenon, which has no counterpart in the classical limit was given [5]. One of the solutions of this obstacle is based on the idea of taking the number of degrees of freedom to infinity [6]. For example, in [7] it was shown that a class of quantum dynamics of harmonic crystals becomes ergodic and mixing in the thermodynamic limit. Moreover, by taking h --> 0, classical properties of ergodicity and mixing are recovered. Similar results, but for the ideal gas quantized according to the Maxwell-Boltzmann statistics, are presented in [8].

Another way to recognize chaotic behavior in quantum systems is to investigate the concept of entropy. Kosloff and Rice [9] introduced a generalization of Kolmogorov-Sinai entropy for the quantum case, which allows to compare the behavior of a given system when described alternatively by classical and quantum mechanics. An even simpler idea was proposed by Thiele and Stone [10]. They suggested that the yon Neumann entropy of the time-averaged density matrix (minus the entropy connected with the preparation of the initial state) can measure quantum chaos. The entropy point of view was taken also in a more recent paper by Slomczynski and Zyczkowski [11]. They considered a pair consisting of a quantum system and a measuring apparatus and proposed a new definition of entropy to measure chaotic behavior of such a coupled system. According to them "the approach linking chaos with the unpredictability of the measurement outcomes is the right one in the quantum case".

On the other hand papers concerning the possible generalization of the notion of Lyapunov exponents have appeared. Because there is no quantum analog of the classical trajectory, the starting point has to be different. Perron-Frobenius operators acting on the space of densities provide a natural frame for the construction of the quantum counterpart of classical characteristic exponents. Such a construction has been carried out for example in [12,13].

In the present paper we will not discuss this interesting subject in general. Leaving aside the problem of existence and definition of an intrinsic quantum chaos, we adopt the point of view of [11] and restrict ourselves to the case of a quantum system interacting with a measuring device, or, more broadly, to quantum open systems. Because, as was shown by Graham [14,15], in a class of such systems the sensitive dependence of some expectation values on initial conditions remains, and the limits t-->oo, h -->0 may commute for a dissipative dynamics, so the notion of chaotic behavior seems to make sense there. Moreover, in the presence of dissipation, coherence effects degrade and give way to an incoherent dynamics closer to the classical behavior. One of the attempts in this direction was the investigation of properties of the quantum survival probability function in open systems [16]. For the following master equation

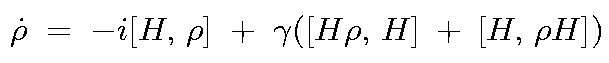
the different behavior in the regular and chaotic cases of the quantum survival probability function averaged over initial conditions and Hamiltonian ensembles was demonstrated. For a general discussion of quantum chaos with dissipation see [17]. A more general approach investigating hypercyclicity and chaos in the context of strongly continuous semigroups of bounded lineal' operators in Banach spaces was proposed in [18]. However, the definition of a chaotic semigroup given there cannot be applied to contractive semigroups such as Perron-Frobenius semigroups acting on the space of densities. In this case the idea of exactness of the system proved to be fruitful in the description of chaotic Markov semigroups associated with some differential equations [19].

In this paper we generalize the notions of completely mixing and exact systems to the quantum level and propose a quantity, the quantum characteristic exponent Aq, which, in the classical case, corresponds to the highest order Lyapunov exponent measuring the speed of convergence of an exact classical system to statistical equilibrium. The property lambda_q > 0 selects a subclass of completely mixing systems which we call exponentially mixing. However, contrary to the classical case, exponentially mixing quantum open systems may not imply chaotic behavior. The relation of lambda_q to that one proposed by Majewski and Kuna in [13] is also discussed. Finally, these concepts are illustrated by the examples of quantum measurements based on event enhanced quantum theory (EEQT).

2. Classical systems
3. Quantum open systems
4. Continuous quantum measurements

Read what's new in the new version (00/05/25)

Download Paper in PDF format (175 kB)

References

[1] Casati G., Quantum mechanics and chaos, in: Chaos and Quantum Physics, eds. M. J. Gianoni, A. Voros and J. Zinn-Justin, North Holland, 1991

[2] Gutzwiller M. C., Chaos in Classical and Quantum Mechanics, Springer, New York, 1990 [3] Alicki R., Makowiec D., Miklaszewski V., Quantum chaos in terms of entropy for periodically kicked top, Phys. Rev. Lett. 75 (1996) 838-841

[4] van Kampen N. G., Quantum chaos as basis for statistical mechanics, in: Chaotic Behaviour in Quantum Systems, ed. G. Casati, Plenum Press, New York, 1985

[5] Jona-Lasinio G., Presilla C., Capasso F., Chaotic quantum phenomena without classical counterpart, Phys. Rev. Lett. 68 (1992) 2269-2272

[6] Jona-Lasinio G., Presilla C., Chaotic properties of quantum many-body systems in the thermodynamic limit, Phys. Rev. Lett. 77 (1996) 4322-4325

[7] Graffi S., and Martinez A., Ergodic properties of infinite quantum harmonic crystals: an analytic approach, J. Math. Phys. 37 (1996) 5111-5135

[8] Lenci M., Ergodic properties of the quantum ideal gas in the Maxwell-Boltzmann statistics, J. Math. Phys. 37 (1996) 5136-5157

[9] Kosloff R., Rice S. A., The influence of quantization on the onset of chaos in Hamiltonian systems: the Kolmogorov entropy interpretation, J. Chem. Phys. 74 (1981) 1340-1349

[10] Thiele E., Stone J., A measure of quantum chaos, J. Chem. Phys. 80 (1984) 5187-5193

[11] Stomczynski W., Zyczkowski K., Quantum chaos: an entropy approach, J. Math. Phys. 35 (1994) 5674-5700

[12] Vilela Mendez R., Entropy and quantum characteristic exponents. Steps towards a quantum Pesin theory, in: Chaos - The Interplay Between Stochastic and Deterministic Behaviour, eds. P. Garbaczewski, M. Wolf and A. Weron, Springer, Berlin, 1995

[13] Majewski W. A., Kuna M., On quantum characteristic exponents, J. Math. Phys. 34 (1993) 5007-5015

[14] Graham R., Chaos in dissipative quantum systems, in: Chaotic Behaviour in Quantum Systems, ed. G. Casati, Plenum Press, New York, 1985

[15] Graham R., Chaos in dissipative quantum maps, in: Quantum Measurement and Chaos, eds. E. R. Pike and S. Sarkar, Plenum Press, New York, 1987

[16] Tameshtit A., Sipe J. E., Survival probability and chaos in an open system, Phys. Rev. A 45 (1992) 8280-8283

[17] Dittrich T., HAnggi P., Ingold G-L., Kramer B., Sch6n G., Zwerger W., Quantum Transport and Dissipation, Wfiey-VCH, Weinheim, 1998

[18] Desch W., Schappacher W., Webb G. F., Hypercyclic and chaotic semi-groups of linear operators, Ergod. Th. & Dynam. Systems 17 (1997) 793-819

[19] Lasota A., Mackey M. C., Chaos, Fractals and Noise. Stochastic Aspects of Dynamics, 2nd ed Springer, New York, 1994

[20] Loskot K., Rudnicki R., Relative entropy and stability of stochastic semi-groups, Ann. Pol. Math. 53 (1991) 139-145

[21] Lichtenberg A. J., Lieberman M. A., Regular and Stochastic Motion, Springer, New York, 1983

[22] Crawford J. D., Cary J. R., Decay of correlations in a chaotic measure-preserving transformations, Physica D 6 (1983) 223-232

[23] Alicki R., Lendi K., Quantum Dynamical Semigroups and Applications, Lect. Notes Phys. 286, 1987

[24] Majewski W. A., Remarks on quantum characteristic exponents, Chaos, Solitons and Fractals 9 (1998) 77-82

[25] Zurek W. H., Paz J. P., Quantum chaos: a decoherent definition, Physica D 83 (1995) 300-308

[26] Blanchard Ph., Jadczyk A., On the interaction between classical and quantum systems, Phys. Lett. A 175 (1993) 157-164

[27] Blanchard Ph., Jadczyk A., Strongly coupled quantum and classical systems and Zeno's effect, Phys. Lett. A 183 (1993) 272-276

[28] Jadczyk A., Kondrat G., Olkiewicz R., On uniqueness of the jump process in event enhanced quantum theory, J. Phys. A 30 (1997) 1863-1880

[29] Blanchard Ph., Jadczyk A., Event enhanced quantum theory and piece-wise deterministic dynamics, Ann. der Physik 4 (1995) 583-599

[30] Jadczyk A., Topics in quantum dynamics, in: Infinite Dimensional Geometry, Noncommutative Geometry, Operator Algebras and Fundamental Interactions, Coquereaux R et al. (eds.), World Scientific, Singapore, 1995

[31] Casati G., Maspero G., Shepelyansky D.L., Quantum fractal eigenstates, Physica D 131 (1999) 311-316

[32] Jastrzebski G., Interacting classical and quantum systems. Chaos from quantum measurements, Ph. D. thesis, University of Wroclaw (in Polish), 1996

[33] Manning A., A relation between Lyapunov exponents, Hausdorff dimension and entropy, Ergod. Th. and Dynam. Systems 1 (1981) 451-459

[34] Young L.-S., Dimension, entropy and Lyapunov exponents Ergod. Th. and Dynam. Systems 2 (1982) 109-124

[35] Misra B., Sudarshan E. C. G., The Zeno's paradox in quantum theory, J. Math. Phys. 18 (1977) 756-763

[36] Pascazio S., Namiki M., Badurek G., Rauch H., Quantum Zeno effect with neutron spin, Phys. Lett. A 179 (1993) 155-160