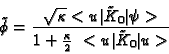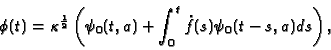GROUP 21

Physical Applications and Mathematical Aspects

of Geometry, Groups, and Algebras

Volume I

Proceedings of the

XXI International Colloquium on

Group Theoretical Methods in Physics

15-20 July 1996 Goslar, Germany

Arnold Sommerfeld Institute

Editors

H. D. Doebner

P. Nattermann

W. Scherer

Technical University of Clausthal, Germany

World Scientific
Singapore - New Jersey - London - Hong Kong

Opening Address

H. D. Doebner

Ladies and Gentlemen, friends and colleagues,

I have the honour and the privilege to open the XXI. International Colloquium on Group Theoretical Methods in Physics as the chairman of the Standing Committee. I welcome you here in Goslar in the name of the organizing committee. As you probably know, the Standing Committee, with presently 18 members, is a kind of umbrella organization for this conference series. The chairman accepts detailed applications from universities and also from other institutions to organize a colloquium. The committee decides by majority vote. In general the site of a colloquium is decided 4 years before the planned date. Certainly, because of their standing, their experience and their feeling for new and interesting developments, the members of the Standing Committee have some influence on the scientific program and it's directions, but only if the local organizers follow their advice.

Together with Peter Kramer we proposed to have the colloquium for the second time in Germany and like the II. Wigner Symposium in Goslar. We expected support of the Technical University of Clausthal and the State Government of Lower Saxony. Under its late chairman, Larry Biedenharn, the Standing Committee decided 1992 in Salamanca in favour of Goslar. That's one of the reasons why you are here?

The series jumped from one continent to the other. We had - not counting the first three small meetings - 8 colloquia in Europe, including the present colloquium in Goslar, 6 in America, 2 in the middle and 2 in the far East. It is now a conference series with tradition and an outstanding international reputation. It is centered around systems in natural science, especially in physics which can be described or modeled through those mathematical methods which are related to symmetries. One of this methods, especially during the first part of the conference series was pure group theory and it's representation theory. This method developed in recent years to the much larger field of a geometrical modeling of complex physical systems - you may call it "Group Theory in its widest sense with all the related algebraic, topological and analytic structures".

The colloquia are a series in physics, in theoretical and in mathematical physics. Mathematics plays a central and essential role. It is a starting point of physical modelings and gains also from their results. Hence in all the colloquia plenaries report on different and interesting fields in physics. In Group 2l we begin with control theory of anholonomic systems and end with a non - commutative change of our space time through gravity. The mathematical parts with a physical bias is strongly represented and we have plenaries in connection with those experiments which verifies our geometrical models.

Following some suggestions of our advisory committee and the Standing Committee, we have under the umbrella of Group 2l three substructures: symposia on quantum groups on aperiodic order and on semi - groups, with co - organizers V Dobrev, A. Bohm and R.V Moody. Group 2l should be more attractive for more specialized physicists and mathematicians working in our field, if they have their own forum. The number of registrations for Group 2l shows that we are right.

We registered more than 380 participants within general interesting abstracts. We decided to have in addition to the plenary talks six parallel sessions with twenty or thirty minute talks, i. e. altogether 272 oral contributions and approximately 90 poster. The decision to have six parallel sessions was not easy. But it seems that the administrations all over the world support travel to conferences only if a lecture is guaranteed; furthermore, posters do not always have the same acceptance as a talk. Nevertheless we hope that we have organized the posters in such a way that they are equally effective and successful as short oral contributions.

We have to thank our sponsors, the German national science foundation (DFG), the state of Lower Saxony, the Technical University of Clausthal, the Arnold Sommerfeld Institute, the German academic exchange service (DAAD) and the Alexander von Humboldt Foundation. We are indebted to the IUPAP for a general sponsorship. My personal thanks go to Wolfgang Scherer and his crew of PhD students of the Arnold Sommerfeld Institute and graduate students for their highly motivated and hard work for Group2l.

I have to add the following: We are living in a changing world; our lifetime is limited. We all know this but the death of a friend, a colleague, a great scientist who changed our view on nature makes us mourning and touches our emotion. Three of our friends and colleagues passed away in the last year: Eugene Wigner, Larry Biedenharn, and Asim Barut.

Please stand up for a moment of silence devoted to their memory.

p.314

Time of Arrival in Event Enhanced Quantum Theory

Philippe Blanchard¹ - Arkadiusz Jadczyk²
¹ Faculty of Physics and BiBoS, University of Bielefeld, Universitätstrasse 25, D 33615 Bielefeld, Germany
²Institute of Theoretical Physics, University of Wroclaw, Pl. Maxa Borna 9, PL-50 204 Wroclaw, Poland; e-mail: ajad@ift.uni.wroc.pl

Abstract:

The new solution to the problem of time of arrival in quantum theory is presented herein. It allows for computer simulation of particle counters and it implies Born's interpretation. It also suggests new experiments that can answer the question: can a quantum particle detect a detector without being detected?

1. Introduction

One of the most troublesome deficiencies of Textbook Quantum Theory is that it leaves questions about timing of experimental events unanswered. The principal reason for this deficiency is that an experimental event (or measurement) can not be defined within the standard theory [1,2]. Due to this deficit, Bell felt the need to introduce beables into quantum theory [3].

Recently we have developed a semi-phenomenological theory that cures this deficiency and also has a predictive power that is stronger than the Standard Quantum Theory. That is why it was entitled Event Enhanced Quantum Theory or, in short, EEQT [4].

EEQT can be thought of as a formalism implementing Bohr's idea that the end result of any experimental event is classical in nature - necessarily - so that we can communicate to our colleagues what we did and what result we obtained. The line separating the quantum from the classical is also known as the Heisenberg cut. EEQT is a semi-phenomenological theory because it considers the exact placement of the cut as a convention. Stapp (see [5] and references therein) believes that the only events that are real are mental (or experiential) events. Pushing the borderline between quantum and classical toward human mind/brain interface would make EEQT into a fundamental theory - provided an exact form of the interface between matter and mind is identified. For most practical purposes, however, the borderline can be placed simply between the quantum object and the classical measuring apparatus or its part (e.g. its display, or pointer). EEQT gives us the mathematical framework to describe the interface and the reciprocal coupling - with information flowing from the quantum system to the classical measuring device and with the unavoidable back action on the quantum system.

What is most important is that EEQT provides the algorithm that enables us to model the individual experiential sequences, including the timing of events. A discussion of other apsects of an evolutionary picture in quantum theory has been given by Haag [6]. Here we will discuss its practical application in the context of time of arrival.

2. Time of arrival: definition

The simplest situation when the question of time of arrival can be discussed is that of a particle moving on a line and we ask at what time the particle will arrive at some specific point on this line. In order to answer this question experimentally we would set a particle detector at and measure the time interval between the moment the particle is released and the moment it is registered by the detector. Experiments suggest is a random variable. After repeating the experiment many times, and assuming the particle is always being prepared in the same quantum state $\vert\psi>$ , we arrive at an experimental probability distribution . We will denote by the probability that the particle is detected up to time , thus

$P(t)=\int_0^t p(s)ds$ .

In practice we do not have 100% efficient detectors, so we have the probability $P(\infty)$ that the detector will detect the particle at all, is less than one. ¹ . The standard quantum theory does not provide us with any formula for .

Wigner (cf. Eq. (5), p. 240 of Ref. [7]) has assumed, completely ad hoc, that the formula

$\begin{displaymath}p(t)= const \vert \psi(a,t)\vert^2, \end{displaymath}$

(1)

where $\psi(t)$ is a solution of the Schrödinger equation. ² One needs, to this end, to go beyond the standard theory and there are not so many options - one can try Nelson's Stochastic Mechanics, Bohmian Mechanics or EEQT. The formula for time of arrival can then serve as an empirical test which can judge which of the alternatives better fits the experimental data.

In the present paper we will follow [8] and describe the formula for time of arrival as predicted by EEQT. In fact, following Wigner, we will consider first a somewhat more general problem, namely that of time of arrival at a given state $\vert u >$ . In EEQT noiseless coupling of a quantum system to a classical yes-no device is described by a positive operator . In our case we take $F={\sqrt \kappa} \vert u><u\vert$ , where $\kappa$ is a phenomenological coupling constant parameter of physical dimension $t^{-1}$ . The Master Equation describing continuous time evolution of statistical states of the quantum system coupled to the detector reads:

$\displaystyle {\dot \rho}_0(t)$	$\textstyle =$	$\displaystyle -{i\over\hbar}[H_0,\rho_0(t)]+F \rho_1 F$
$\displaystyle {\dot \rho}_1(t)$	$\textstyle =$	$\displaystyle -{i\over\hbar}[H_1,\rho_1]-{1\over2} \{F^2,\rho_1\}.$	(2)

Suppose at the detector is off, that is in the state denoted by , and the particle state is $\vert \psi>$ , with $<\psi\vert\psi>=1.$ Then, according to EEQT (cf. [4,8]) the probability of detection, that is of a change of state of the detector, during time interval is equal to $1-<\psi\vert K(t)^\star K(t)\vert\psi>$ , where

$\begin{displaymath}K(t)=\exp (-{i\over\hbar}H t-{F^2\over2}t). \end{displaymath}$

(3)

It then follows that the probability that the detector will be triggered out in the time interval (t,t+dt), provided it was not triggered yet, is given by

$\begin{displaymath} p(t)={d\over{dt}}P(t)=\kappa\ \vert <u\vert K(t)\vert \psi>\vert^2. \end{displaymath}$

(4)

The difference between the above and Wigner's formula is presence of the coupling constant $\kappa$ as well as the damping term in the definition of the propagator . It is this damping term together with the coupling constant that assure that $P(\infty) \leq 1$ in contrast to the formula as in [7].
To compute let us note that is equal to $\vert \phi(t)\vert^2$ , where the complex amplitude $\phi(t)$ is given by $<u\vert K(t)\vert \psi>$ . Denoting by ${\tilde \phi(z)}$ the Laplace transform of $\phi(t)$ one easily gets (cf [8]):

$\begin{displaymath} {\tilde\phi}={{\sqrt\kappa}<u\vert{\tilde K_0}\vert\psi> \over{1+{{\kappa\over2}\ <u\vert{\tilde K}_0\vert u>}}} \end{displaymath}$

(5)

where

$\begin{displaymath}K_0(t)=\exp (-{i\over\hbar}H t). \end{displaymath}$

(6)

This is our final formula for the Laplace transform of the probability amplitude of time of arrival.

**Figure 1:** Probability density of time of arrival for a point counter placed at , dimensionless coupling constant $\alpha=m\eta\kappa/\hbar$ . The incoming Gaussian wave packet of width $\eta$ starts at , $x=-8\eta$ , with velocity $v=2\hbar/m\eta$

Let us consider a free Schrödinger particle on a line, and let us take to denote the improper position eigenstate at , that is $<x\vert u>=\delta(x-a)$ . Then

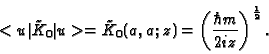
$\begin{displaymath}<u\vert{\tilde K}_0\vert u>= {\tilde K}_0(a,a;z)=\left({\hbar m\over{2iz}}\right)^{1\over2}. \end{displaymath}$

(7)

Let us denote:

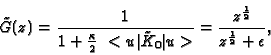
$\begin{displaymath}{\tilde G}(z)={1\over{1+{{\kappa\over2}\ <u\vert{\tilde K}_0\vert u>}}}= {{z^{1\over2}}\over {z^{1\over2}+\epsilon}}, \end{displaymath}$

(8)

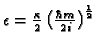where $\epsilon={\kappa\over2}\left( {{\hbar m}\over{2i}} \right)^{1\over2}$ It can be now checked that the inverse Laplace transform

of ${\tilde G}(z)$ is given by

$\begin{displaymath} G(t)=\delta(t)+{d\over{dt}}f(t), \end{displaymath}$

(9)

where

$\begin{displaymath} f(t)=e^{\epsilon^2t} \mbox{Erfc} \left(\epsilon t^{1\over2}\right). \end{displaymath}$

(10)

The amplitude $\phi(t)$ becomes then:

$\begin{displaymath} \phi(t)=\kappa^{1\over2}\left(\psi_0(t,a)+\int_0^ t{\dot f}(s)\psi_0(t-s,a) ds\right), \end{displaymath}$

(11)

where $\psi_0$ stands for the freely evolving wave function. The second term in the formula (11) gives the necessary correction to the Wigner formula (1).

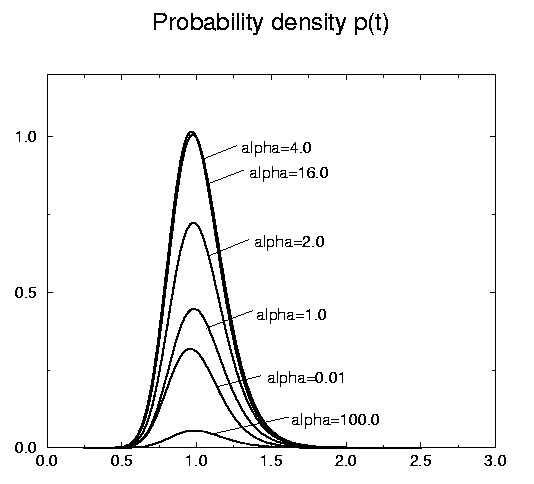
It is instructive to discuss the limit of infinite coupling constant. Numerical simulations show that for every incoming wave packet there is an optimal value of the coupling constant $\kappa$ which gives the maximal efficiency of the detector. Increasing $\kappa$ over this optimal value causes loss of efficiency because of reflection of the particle by the detector. In the limit of infinite $\kappa$ the detector efficiency $P(\infty)$ drops to zero - cf. Fig 1. One may ask what is the maximum value of the efficiency $P(\infty)$ for a point counter? We do not know the answer to this question. Our guess is that the maximum efficiency is reached for a Gaussian wave packet that is placed centrally over the detector with zero velocity. Numerical simulations seems to confirm this guess. The wave packet slowly spreads out being at the same time "eaten" by the sink at its center. Figure 2 shows the dependence of the detector efficiency on the value of the dimensionless coupling constant $\alpha=m\eta\kappa/\hbar$ . The maximum is attained at the value of $\alpha\approx 1.3216$ and turns out to be $\approx 1.73$ .

**Figure:** Optimal coupling constant as a function of velocity of the incoming wave packet. The dependence pretty soon saturates to a linear one. At the saturation value $P(\infty)\asymp 0.5.$

It would be desirable to have an analytical proof or disproof of our conjecture. The fact that the maximal detector efficiency is less than one may seem to be an artefact of the singular character of a pointlike detector. It may, however, also have some deeper meaning. If so, then such a meaning is not known to us.

3. Conclusions

We have seen that the formula for time of arrival of a Schrödinger particle contains a phenomenological parameter $\kappa$ characterizing the strength of the coupling between the particle and the sink. If $\kappa$ is too small then most of the particles would pass the detector undetected. If $\kappa$ is too big, then the sink will also act as a reflecting barrier. For each incoming wave packet there is an optimal value of the coupling that gives maximal detector efficiency.

Our formula for the time of arrival can be used to perform again Wigner's analysis of time-energy uncertainty relation. However, it must be noticed that the correct analysis will be much more difficult than that in the original Wigner's paper [7]. First of all our formula (11) contains an extra term which is absent in the Wigner paper. Second, in case of a general time of arrival at a state $\vert u>$ Wigner's formula for spread $\epsilon^2$ given by his Eq. (5b) of Ref. [7] is also incorrect as his "or" between Eq. (2) and Eq. (2a) does not hold for a general $\vert u>$ .

From the probabilistic point of view the process of arrival of a quantum system at a given state $\vert u>$ is an inhomogeneous Poisson process with the rate function

$\begin{displaymath}\lambda (t) = \kappa\ {{<\psi\vert K(t)^\star\vert u><u\vert K(t)\vert\psi>}\over {<\psi\vert K(t)^\star K(t)\vert\psi>}}. \end{displaymath}$

(12)

A more general algorithm for a piecewise deterministic process describing individual sample path during a continuous measurement can be found in Ref. [4].

It is to be stressed that the damping term in the propagator (cf. Eq. (3) is to be thought of as experimentally verifiable. That is, the very presence of a detector, even if the particle goes through it undetected, changes the time evolution of the wave packet by adding imaginary potential to the Hamiltonian. The phenomenon here is of the same kind as that discussed by Dicke [9], Elitzur et al. [10] and Kwiat et al. in [11]. We can say that the particle can detect a detector without being detected itself . Our formula for describes this effect in a quantitative way.

Finally, let us note that it would be interesting to obtain a relativistic version of the time of arrival formula. This can be in principle done by exploiting the ideas given in Ref. [12].

Acknowledgments

One of us (A.J.) would like to thank A. von Humboldt Foundation for the support, and to Laura. Knight for reading the manuscript.

Bibliography

1: Bell, J.: `Towards an exact quantum mechanics', in Themes in Contemporary Physics II. Essays in honor of Julian Schwinger's 70th birthday, Deser, S. , and Finkelstein, R. J. Ed. , World Scientific, Singapore 1989
2: Bell, J.: ` Against measurement', in Sixty-Two Years of Uncertainty. Historical, Philosophical and Physical Inquiries into the Foundations of Quantum Mechanics, Proceedings of a NATO Advanced Study Institute, August 5-15, Erice, Ed. Arthur I. Miller, NATO ASI Series B vol. 226 , Plenum Press, New York 1990
3: Bell, J.:`Beables for quantum theory', in Speakable and unspeakable in quantum mechanics, Cambridge University Press 1987
4: Blanchard, Ph., and A. Jadczyk: `Event-Enhanced-Quantum Theory and Piecewise Deterministic Dynamics', Ann. der Physik 4 (1995) 583-599; see also the short version: `Event and Piecewise Deterministic Dynamics in Event-Enhanced Quantum Theory' , Phys.Lett. A 203 (1995) 260-266
5: Stapp, H.P.: ` Science of Consciousness and the Hard Problem' , Preprint LBL-38621, Lawrence Berkeley Lab., May 31, 1996
6: Haag, R.: `An Evolutionary Picture for Quantum Physics', Commun. Math. Phys. 180, (1996) 733-743
7: Wigner, E.P.: `On the Time-Energy Uncertainty Relation', in Aspects of Quantum Theory, Ed. Salam, E., and Wigner, E.P. , Cambridge University Press, Cambridge 1972
8: Blanchard, Ph., and A. Jadczyk: `Time of Events in Quantum Theory', Helv. Phys. Acta 69 (1996) 613-635
9: Dicke, R.H.: `Interaction-free quantum measurements: A paradox? ', Am. J. Phys 49 (1981) 925-930
10: Elitzur, A., Vaidman, L.: `Quantum Mechanical Interaction-Free Measurements', Found. Phys 23 (1993) 987-997
11: Kwiat, P., Weinfurter, H., Herzog, T, Zeilinger, A.: ` Interaction-Free Measurement', Phys. Rev. Lett. 74 (1995) 4763-4766
12: Blanchard, Ph., and A. Jadczyk: `Relativistic Quantum Events', Found. Phys. 26 (1966), 1669-1681

Footnotes

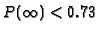
... one. ¹: Anticipating the following discussion let us mention at this place that numerical simulations using our formula for time arrival for a point-like detector suggests $P(\infty)< 0.73$
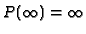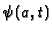... equation. ²: This formula is evidently wrong as it leads, for a Gaussian wave packet, to $P(\infty)=\infty$ . Later on we will see that the correct formula (cf. Eq.(4)) involves integral transform of $\psi(a,t)$ .