Let us consider the simplest case: that of a two-state classical system. We
call its two states "off" and "on." Its
action is simple: if it is off, then it will stay off forever. If it
is on, then it can detect a particle and go off. Later on we will
specialize to detection
of particle presence at a given location in space.
For a while let us be
general and assume that we have two Hilbert spaces ![]() and two Hamiltonians
and two Hamiltonians ![]() . We also have a time dependent family of
operators
. We also have a time dependent family of
operators ![]() and let us denote
and let us denote
![]() .
According to
the theory presented in the previous section, with
.
According to
the theory presented in the previous section, with ![]() ,
, ![]() ,
the master equation for the total system, i.e. for particle and detector,
reads:
,
the master equation for the total system, i.e. for particle and detector,
reads:
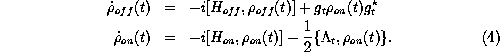
Suppose at t=0 the detector is "on" and the particle state is
![]() , with
, with ![]() Then, according to the event generating algorithm
described in the previous section, probability of detection during
time interval (0,t) is equal to
Then, according to the event generating algorithm
described in the previous section, probability of detection during
time interval (0,t) is equal to ![]()
Let us now specialize and consider a detector of particle present at a location a in space (of n dimensions). Our detector has a certain range of detection and certain efficiency. We encode these detector characteristics in a gaussian function:
![]()
If the detector is moving in space along some trajectory a(t), and if
the detector characteristics are constant in time, then we put:
![]() .
Let us suppose that the detector is off at
.
Let us suppose that the detector is off at ![]() and that the
particle wave function is
and that the
particle wave function is ![]() . Then, according to the
algorithm described in the previous section, probability of detection
in the infinitesimal time interval
. Then, according to the
algorithm described in the previous section, probability of detection
in the infinitesimal time interval ![]() equals
equals
![]() . In the limit
. In the limit
![]() , when
, when ![]() we get
we get ![]() . Thus we recover the
usual Born interpretation, with the evident and necessary correction that
the probability of detection is proportional to the length of exposure
time of the detector.
. Thus we recover the
usual Born interpretation, with the evident and necessary correction that
the probability of detection is proportional to the length of exposure
time of the detector.
That simple formula holds only for short exposure times. For a prolonged
detection, the formula becomes more involved, primarily
because of non-unitary evolution due to the presence of the detector. In that
case, numerical simulation is necessary. To
get an idea of what happens, let us consider a simplified case which
can be solved exactly. We will consider the ultra-relativistic Hamiltonian
H=-i d/dx in space of one dimension.
In that case the non-unitary evolution equation is easily solved:
![]()
In the limit ![]() when the detector shrinks to a point,
and assuming that this point is fixed in space a(t)=a,
we obtain for the probability p(t) of detecting the particle in the time
interval (0,t):
when the detector shrinks to a point,
and assuming that this point is fixed in space a(t)=a,
we obtain for the probability p(t) of detecting the particle in the time
interval (0,t):
![]()
Intuitively this result is very clear. Our Hamiltonian describes
a particle moving to the right with velocity c=1, the shape of the
wave packet is preserved. Then p(t) is equal to the probability that
the particle at t=0 was in a region of space that guaranteed passing
the detector, multiplied by the detector efficiency factor - in our case
this factor is ![]()