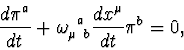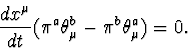Institut für Theoretische Physik
der Universität Goettingen
Bunsenstrasse 9, D 3400 Göttingen
Abstract:
Author's comments:
This paper was send for publication in February 1984. It then took almost a year to get Referee Report. Here its is:
This paper contains a summary of some of the known aspects of gravity as a gauge theory and addresses, without substantive results, the phenomena associated with regions where the vierbein vanishes. What is new in the paper is connected with this latter question, but I find the discussion misleading and in any case not sufficiently well developed to justify publication in the paper's present form. Coordinate regions where the metric or vierbein vanishes must be treated with considerable care, as there are generally identifications of points to be taken into account. Pictures such as that of Fig. 2 are thus very misleading. The vanishing of the vierbein is not in general a coordinate-independent statement and what seems to be two points in one coordinate frame could well be seen to be just one in another. This is the case, e.g., with a uniformly accelerated frame in the x direction, where all points withand
finite are to be identified.
December 17, 1984
My comments on the above report - as of today September 18, 1999:
In retrospect, I realize that the anonymous referee did not, in fact, reject the paper. He suggested that it did not justify publication in its present form. However, I was sufficiently discouraged by his comments to decide not to work on improving the form any further. Also in retrospect, it seems clear that the referee missed my point: when all the information that we have is included in the metric then, we can try to play the game of identifying the points to get rid of the "singularity." But within the framework I was discussing in this paper, there was also a principal connection using extra dimensions and giving extra-information. Gluing some space-time points together would create discontinuity of the connection. Vierbein, in the paper, was defined as one-form with values in an associated vector bundle and its vanishing was a coordinate independent statement. Yet, the referee was right on one point: the ideas of the paper could have been developed better. Although I have shied away from the subject in the intervening years, at the time I was suggesting that "faster-than-light teleportation" is possible but, indeed, I failed to provide the explicit description of a transdimensional remolecularizer working on this principle.
In the meantime the paper has been quoted in I. Bengtsson, "Degenerate metrics and an empty black hole", Class. Quantum Grav. 8 1991, 1847-1857 (for more recent developments cf. also I. Bengtsson and T. Jacobson, "Degenerate metric phase boundaries", Class. Quantum Grav. 14 1997, 3109-3121
1. Introduction
Hanson and Regge [1] (see also D'Auria and Regge [2] ) suggested that a gravitational Meissner effect might
exist producing torsion vortices accompanied by vanishing of a vierbein.
This in turn may indicate a phenomenon of "unglueing" of a principal ![]() (or
(or ![]() ) bundle from the bundle of frames of the space-time manifold
) bundle from the bundle of frames of the space-time manifold
![]() The idea that a proper arena for gauge theories of gravitation is
an external principal bundle
The idea that a proper arena for gauge theories of gravitation is
an external principal bundle ![]() over
over ![]() rather than the frame bundle
rather than the frame bundle ![]() of
of ![]() has been put forward by many authors (see e.g. [3,4,5]). It is not our aim to justify this belief here. In
fact what is relevant is not so much the choice of a bundle but the choice
of dynamical variables and their dynamics. As long as a vierbein is thought
of as representing a homomorphism of the two bundles, any distinction
between
has been put forward by many authors (see e.g. [3,4,5]). It is not our aim to justify this belief here. In
fact what is relevant is not so much the choice of a bundle but the choice
of dynamical variables and their dynamics. As long as a vierbein is thought
of as representing a homomorphism of the two bundles, any distinction
between ![]() and a subbundle of
and a subbundle of ![]() does not really matter. The distinction becomes important when the
vierbein is interpreted as a linear map
does not really matter. The distinction becomes important when the
vierbein is interpreted as a linear map
![]() from the tangent
spaces of
from the tangent
spaces of ![]() into the fibers of a vector bundle associated with
into the fibers of a vector bundle associated with ![]() Such an interpretation is natural in gauge theories of the Poincaré
group
Such an interpretation is natural in gauge theories of the Poincaré
group ![]() (see e.g. [4,5,6]) and of
(see e.g. [4,5,6]) and of ![]() [8], where
[8], where ![]() appears as a composite object.
appears as a composite object.
The paper is organized as follows. in Sect. 3 we formulate a gauge theory
of the Lorentz group and point out that the requirement of smoothness
of the Lagrangian at a degenerate vierbein is a strong selection criterion.
Only three terms survive the test, one of them having a "wrong parity",
and two others are (cosmetically improved) the standard Einstein-Hilbert
Lagrangian and the cosmological term. In Sect. 4 we briefly discuss the
structure of the gauge theory of the Poincare group, and of the ![]() gauge theory considered by Stelle and West [8]. In Sect. 5 we analyse relations between these abstract
gauge theories and the conventional ones based on metric tensor and an
affine connection. The relation can be visualized as follows. In an open
region where the vierbein
gauge theory considered by Stelle and West [8]. In Sect. 5 we analyse relations between these abstract
gauge theories and the conventional ones based on metric tensor and an
affine connection. The relation can be visualized as follows. In an open
region where the vierbein ![]() is nondegenerate the external bundle is glued with the help of
is nondegenerate the external bundle is glued with the help of
![]() to the frame bundle and the bundle connection can be interpreted
as an affine connection on
to the frame bundle and the bundle connection can be interpreted
as an affine connection on ![]() . When
. When ![]() becomes degenerate the external bundle detaches from the frame
bundle. The principal connection chooses to live in the external bundle
and the affine connection dies. Two examples are given in Sect. 6 . The
first is a kind of gravitational instanton considered by Hanson and Regge
[1] and D'Auria and Regge [2]. A zero of a vierbein is accompanied by non-zero torsion.
The second example is an adaptation of a model discussed by Einstein and
Rosen [9]. The vierbein vanishes here on a 3-dimensional "bridge"
connecting two mirror copies of the exterior Schwarzschild universe. It
is interesting to notice that the principal connection continues smoothly
over the bridge and need not be regularized as in the first example. The
Einstein-Rosen bridge is therefore a torsion-free regular solution of
vacuum field equations of
becomes degenerate the external bundle detaches from the frame
bundle. The principal connection chooses to live in the external bundle
and the affine connection dies. Two examples are given in Sect. 6 . The
first is a kind of gravitational instanton considered by Hanson and Regge
[1] and D'Auria and Regge [2]. A zero of a vierbein is accompanied by non-zero torsion.
The second example is an adaptation of a model discussed by Einstein and
Rosen [9]. The vierbein vanishes here on a 3-dimensional "bridge"
connecting two mirror copies of the exterior Schwarzschild universe. It
is interesting to notice that the principal connection continues smoothly
over the bridge and need not be regularized as in the first example. The
Einstein-Rosen bridge is therefore a torsion-free regular solution of
vacuum field equations of ![]() gauge theory.
gauge theory.
It was pointed out in [2] that "the vanishing vierbein at some point is not a disastrous feature of theory". It is one of the aims of the present note to point out that with an appropriate dynamics vanishing vierbein in a whole region need not be a disaster either. It is shown in Sect. 7 that such a "dead" region can have observable effects seen from outside, and that it introdu ces statistical elements (that is "freedom of choice") already on a classical level.
2. Notation
Let ![]() be a principal bundle, let
be a principal bundle, let ![]() be a representation of
be a representation of ![]() on a vector space
on a vector space ![]() and let
and let ![]() denote the derived representation of the Lie algebra
denote the derived representation of the Lie algebra ![]() of
of ![]() . For every
. For every ![]() let
let ![]() denote the fundamental vector field on
denote the fundamental vector field on ![]() generated by
generated by ![]() An
An ![]() -valued
-valued ![]() -form,
-form, ![]() ,
, ![]() on
on ![]() is called tensorial of type
is called tensorial of type ![]() if
if
![]() and
and
![]() for all
for all ![]() (see [10, p. 75] ). Let
(see [10, p. 75] ). Let
![]() be the vector bundle associated with
be the vector bundle associated with ![]() via the representation
via the representation ![]() ( [10, p. 55] ). One can identify
( [10, p. 55] ). One can identify ![]() -valued tensorial
-valued tensorial ![]() -forms of type
-forms of type ![]() on
on ![]() with
with ![]() -valued
-valued ![]() -forms on
-forms on ![]() (see [10, p. 76], [12, Ch. VII. 1], [11, Ch XX. 5]). This identification is extensively used
in the literature and we shall use it too without further references.
In particular the curvature 2-form
(see [10, p. 76], [12, Ch. VII. 1], [11, Ch XX. 5]). This identification is extensively used
in the literature and we shall use it too without further references.
In particular the curvature 2-form
![]() of a principal connection
of a principal connection ![]() on
on ![]() can be thought of as a 2-form on
can be thought of as a 2-form on ![]() with values in
with values in ![]() , where
, where ![]() denotes the adjoint representation of
denotes the adjoint representation of ![]() on
on ![]()
3.  gauge theory
gauge theory
Let
![]() be a principal bundle over a
be a principal bundle over a ![]() -dimensional base manifold
-dimensional base manifold ![]() The fibers of
The fibers of ![]() are to be thought of as being a priori completely detached from fibers
of the frame bundle of
are to be thought of as being a priori completely detached from fibers
of the frame bundle of ![]() Let
Let ![]() denote the natural representation of
denote the natural representation of ![]() on
on ![]() . The dynamical variables of a generalized Einstein-Cartan
theory are: a principal connection
. The dynamical variables of a generalized Einstein-Cartan
theory are: a principal connection ![]() on
on ![]() , and a
, and a ![]() -valued
-valued ![]() -form
-form ![]() on
on ![]() In a "pure gauge theory" 3 a Lagrangian
In a "pure gauge theory" 3 a Lagrangian ![]() -form should be constructed out of
-form should be constructed out of ![]() and
and ![]() alone. We demand that the action should be a smooth (and thus
nonsingular) function of field configuration variables
alone. We demand that the action should be a smooth (and thus
nonsingular) function of field configuration variables
![]() In particular
In particular ![]() should be continuous at
should be continuous at ![]() Among geometrical objects at our disposal we find only six
candidates which have this property:
Among geometrical objects at our disposal we find only six
candidates which have this property:
| (1) | |||
| (2) | |||
| (3) | |||
| (4) | |||
| (5) | |||
| (6) |
Variations of ![]() and
and ![]() are exact
are exact ![]() -forms and do not contribute to classical field equations. Owing to
the first Bianchi identity
-forms and do not contribute to classical field equations. Owing to
the first Bianchi identity ![]() differs from
differs from ![]() by an exact form only.
by an exact form only. ![]() has internal parity different from that of
has internal parity different from that of ![]() and
and ![]() , and should not be combined with them unless
, and should not be combined with them unless ![]() is reduced to
is reduced to ![]() , which would imply dynamically preferred orientation of
, which would imply dynamically preferred orientation of ![]() - a viable possibility.4 Introducing arbitrary coupling constants
- a viable possibility.4 Introducing arbitrary coupling constants
![]() , Euler-Lagrange equations for
, Euler-Lagrange equations for
are:
where ![]() and
and ![]() are
are ![]() -forms representing the sources: energy-momentum and spin. It is important
to notice that field equations (8) and (9)
make sense for all smooth configurations
-forms representing the sources: energy-momentum and spin. It is important
to notice that field equations (8) and (9)
make sense for all smooth configurations
![]() , in particular for those with degenerate
, in particular for those with degenerate ![]() -s. However, the predictive power of these equations falls down
with the rank of
-s. However, the predictive power of these equations falls down
with the rank of ![]() .
.
4. Gauge theories of  and
and 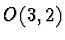
Replacing ![]() with
with ![]() one gets a gauge theory of the Poincaré group. The two
important representations of
one gets a gauge theory of the Poincaré group. The two
important representations of ![]() on
on ![]() are
are
![]() and
and
![]() The dynamical variables of an
The dynamical variables of an
![]() gauge theory are (cf. [4,5]): a principal connection
gauge theory are (cf. [4,5]): a principal connection ![]() on
on
![]() , and a
, and a ![]() -valued
-valued ![]() -form
-form ![]() on
on ![]()
![]() being the affine bundle over
being the affine bundle over ![]() associated to
associated to ![]() The admissible Lagrangians are those of the
The admissible Lagrangians are those of the ![]() gauge theory but now
gauge theory but now ![]() is not a primitive field - it is defined by
is not a primitive field - it is defined by ![]() . Given a field configuration
. Given a field configuration
![]() one can always adapt a gauge (that is to use the translational
freedom and choose a cross section of the principal
one can always adapt a gauge (that is to use the translational
freedom and choose a cross section of the principal ![]() bundle) in such a way that
bundle) in such a way that
![]() - thus, effectively, eliminating the field
- thus, effectively, eliminating the field ![]() from the theory. In this gauge the soldering form
from the theory. In this gauge the soldering form ![]() , defined above as
, defined above as
![]() , coincides with the translational part
, coincides with the translational part ![]() of the connection
of the connection ![]() This closes our discussion of the Poincaré group gauge
theory: after gauge fixing it effectively reduces to Lorentz group gauge
theory.
This closes our discussion of the Poincaré group gauge
theory: after gauge fixing it effectively reduces to Lorentz group gauge
theory.
Another viable possibility is a gauge theory of ![]() , with five dimensional fibres, as discussed in [8]. The dynamical variables of this theory are: an
, with five dimensional fibres, as discussed in [8]. The dynamical variables of this theory are: an
![]() - connection
- connection ![]() and a
and a ![]() -valued
-valued ![]() -form
-form ![]() where
where ![]() denotes the natural representation of
denotes the natural representation of ![]() on
on ![]() The Lagrangian 4-form is [8]
The Lagrangian 4-form is [8]
| (10) |
together with a constraint
| (11) |
Given a configuration ![]() one can always adapt gauge in such a way that
one can always adapt gauge in such a way that ![]() The (generalized) vierbein
The (generalized) vierbein ![]() can be defined by imposing the condition
can be defined by imposing the condition
| (12) |
in the adapted gauge.
5. Relation to metric-affine theories
Let
![]() be a field configuration of an
be a field configuration of an ![]() gauge theory as discussed in Sect. 3. A point
gauge theory as discussed in Sect. 3. A point ![]() is said to be a critical point of
is said to be a critical point of ![]() if
if
![]() otherwise
otherwise ![]() is called a regular point. The set
is called a regular point. The set ![]() of all regular points of a smooth
of all regular points of a smooth ![]() is an open subset of
is an open subset of ![]() When
When
![]() then
then ![]() is called degenerate. A linear space-time connection
is called degenerate. A linear space-time connection ![]() in
in ![]() (sometimes also called an affine connection on
(sometimes also called an affine connection on ![]() ; notice that we admit torsion here) is said to be compatible
with a given field configuration
; notice that we admit torsion here) is said to be compatible
with a given field configuration
![]() if
if
i. e. if ![]() is parallel with respect to
is parallel with respect to
![]() when considered as a cross section of the fiber product
when considered as a cross section of the fiber product
![]() We have then
We have then
and so the ![]() - valued
- valued ![]() -form
-form
![]() may be considered as a generalized torsion.
may be considered as a generalized torsion.
Given a configuration
![]() there exists a unique
there exists a unique ![]() on
on ![]() ,
, ![]() being the open submanifold of
being the open submanifold of ![]() consisting of all regular points of the vierbein, compatible with
consisting of all regular points of the vierbein, compatible with
![]() Outside of
Outside of ![]() - on the set of critical space-time points - the affine connection
- on the set of critical space-time points - the affine connection
![]() will not, in general, exist. To see this observe that at regular
point we have, as a consequence of Eq. (13):
will not, in general, exist. To see this observe that at regular
point we have, as a consequence of Eq. (13):
where
![]() are the coefficients of
are the coefficients of ![]() in a coordinate system
in a coordinate system ![]() From Eq. (13) we get
From Eq. (13) we get
so that the part of ![]() which is responsible for the parallel transport of the length
scale depends on the vierbein only (and not on the connection
which is responsible for the parallel transport of the length
scale depends on the vierbein only (and not on the connection ![]() ). When
). When ![]() becomes degenerate then
becomes degenerate then
![]() , and therefore also
, and therefore also ![]() , diverge. If
, diverge. If ![]() is identically zero then the argument does not apply, and inside
such a region any affine connection is compatible with such a configuration.
is identically zero then the argument does not apply, and inside
such a region any affine connection is compatible with such a configuration.
For every configuration
![]() one defines a covariant "metric" tensor
one defines a covariant "metric" tensor
![]() where
where
![]() is the diagonal constant matrix. The induced
scalar product in
is the diagonal constant matrix. The induced
scalar product in ![]() is nondegenerate if and only if
is nondegenerate if and only if ![]() is regular. On
is regular. On ![]() we have then
we have then
![]() , where
, where ![]() is a unique affine connection compatible with
is a unique affine connection compatible with
![]() . The standard Einstein-Hilbert Lagrangian density
. The standard Einstein-Hilbert Lagrangian density ![]() of
of ![]() is
is
where ![]() is the scalar curvature of
is the scalar curvature of ![]() . One easily finds that
. One easily finds that
where ![]() denotes the
denotes the ![]() - component of a
- component of a ![]() -form
-form ![]() .
.
The identity (18) holds on ![]() . Outside of this region the left hand side of Eq. (18)
is not defined. The right hand side is "almost" defined - if not for the
. Outside of this region the left hand side of Eq. (18)
is not defined. The right hand side is "almost" defined - if not for the
![]() . It is thus clear why taking (7)
for the Lagrangian four-form is a better choice.
. It is thus clear why taking (7)
for the Lagrangian four-form is a better choice.
6. Two examples of configurations with degenerate vierbein
Example 1.: Hanson and Regge [1] (see also [2]) consider an ![]() - thus Euclidean - version of Einstein-Cartan gauge theory. The
base manifold
- thus Euclidean - version of Einstein-Cartan gauge theory. The
base manifold ![]() is
is ![]() and the vierbein
and the vierbein
![]() is defined by
is defined by
| (19) |
| (20) |
It is nondegenerate everywhere except at the origin where it vanishes.
The unique torsion-free connection form (compatible with ![]() )
) ![]() given in
given in
![]() by
by
is flat and singular at ![]() A regularization
A regularization
| (22) |
results in a non-zero torsion
| (23) |
Thus we get a globally defined non-singular connection in an external
![]() bundle. It induces space-time affine connection everywhere except
at the origin. The induced connection has non-vanishing torsion.
bundle. It induces space-time affine connection everywhere except
at the origin. The induced connection has non-vanishing torsion.
Example 2.: Einstein and Rosen [9] considered two examples of solutions of (modified) vacuum
field equations of general relativity with a degenerate metric. Let us
show how both examples can be easily reformulated in terms of an ![]() gauge theory. The first model discussed in [9] describes a uniformly accelerated frame in a flat Minkowski
space. The second, described below, brings similar features with a non-flat
connection. One takes here
gauge theory. The first model discussed in [9] describes a uniformly accelerated frame in a flat Minkowski
space. The second, described below, brings similar features with a non-flat
connection. One takes here
![]() with coordinates
with coordinates
![]() , and the vierbein is given by
, and the vierbein is given by
It degenerates at ![]() (the "bridge"). The connection form can be represented by
(the "bridge"). The connection form can be represented by
At first sight it seems that ![]() is singular on the bridge in an analogy to (21).
However, since the vierbein is degenerate, the
is singular on the bridge in an analogy to (21).
However, since the vierbein is degenerate, the ![]() -forms
-forms ![]() do not form a basis at
do not form a basis at ![]() and therefore not every
and therefore not every ![]() -form can be represented in terms of
-form can be represented in terms of ![]() -s. In fact, we have
-s. In fact, we have
| (24) |
Torsion vanishes here, but ![]() is non-flat. This configuration
is non-flat. This configuration
![]() is a smooth solution of the vacuum (that is with right
hand sides vanishing) field equations (8), (9)
with
is a smooth solution of the vacuum (that is with right
hand sides vanishing) field equations (8), (9)
with
![]()
7. Physical effects of a vanishing vierbein
We have seen that certain Lagrangians are smooth functions of configurations
![]() even for degenerate
even for degenerate ![]() -s, The requirement of smoothness is a strong selection criterion.
In particular it rules out quadratic terms essential in theories with propagating
torsion [15]. It has to be understood whether a singularity at
-s, The requirement of smoothness is a strong selection criterion.
In particular it rules out quadratic terms essential in theories with propagating
torsion [15]. It has to be understood whether a singularity at
![]() stabilizes a theory. Stability properties of metric theories
of gravitation have been discussed by many authors [16]. Theories admitting vanishing vierbein need, however,
special considerations. Hanson and Regge [1] speculated about a possibility of having a "torsion
foam" - a region with vanishing vierbein and well defined principal connection.
No dynamical mechanism which would make such configurations stable is known.
Nevertheless it can be interesting to look for a possible method of detecting
such a phenomenon. Here we discuss motion of a test particle which meets
on its way a domain with vanishing vierbein.
stabilizes a theory. Stability properties of metric theories
of gravitation have been discussed by many authors [16]. Theories admitting vanishing vierbein need, however,
special considerations. Hanson and Regge [1] speculated about a possibility of having a "torsion
foam" - a region with vanishing vierbein and well defined principal connection.
No dynamical mechanism which would make such configurations stable is known.
Nevertheless it can be interesting to look for a possible method of detecting
such a phenomenon. Here we discuss motion of a test particle which meets
on its way a domain with vanishing vierbein.
Consider scattering of spinless particles on a double-cone shaped region
where the vierbein vanishes (see Fig. 1). Equations of motion for a non-spinning
test particle are (see [17])
Notice that four-momentum ![]() and four-velocity
and four-velocity
![]() are a priori considered as independent variables.
It is only through equation (26) that momentum
becomes co-linear with velocity, but this co-linearity needs to obeyed
at regular space-time only. Not inside of the vanishing vierbein domain.
are a priori considered as independent variables.
It is only through equation (26) that momentum
becomes co-linear with velocity, but this co-linearity needs to obeyed
at regular space-time only. Not inside of the vanishing vierbein domain.
In our case, in regions ![]() and
and ![]() , where
, where ![]() is invertible, momentum must be proportional to the velocity,
as it follows from Eq. (26). In consequence
trajectories
is invertible, momentum must be proportional to the velocity,
as it follows from Eq. (26). In consequence
trajectories ![]() and
and ![]() are geodesics. In region
are geodesics. In region ![]() , where
, where ![]() degenerates, momentum and velocity may be totally decoupled.
Let
degenerates, momentum and velocity may be totally decoupled.
Let
![]() (resp.
(resp.
![]() ) denote the position and momentum of the particle
when it enters (resp. leaves) vanishing-vierbein region
) denote the position and momentum of the particle
when it enters (resp. leaves) vanishing-vierbein region ![]() . For given
. For given
![]() denote by
denote by
![]() the collection of all continuous
paths
the collection of all continuous
paths
![]() with the following property:
with the following property: ![]() when paralelly transported along
when paralelly transported along ![]() from
from ![]() to
to ![]() coincides with
coincides with ![]() . Observe that a past trajectory
. Observe that a past trajectory ![]() , and the future trajectory
, and the future trajectory ![]() are uniquely determined by
are uniquely determined by
![]() and
and
![]() respectively. Observe also that two trajectories
respectively. Observe also that two trajectories ![]() and
and
![]() both belong
both belong
![]() if and only if
if and only if ![]() is an eigenvector belonging to the eigenvalue zero of the flux
of the curvature operator through the surface enclosed between
is an eigenvector belonging to the eigenvalue zero of the flux
of the curvature operator through the surface enclosed between ![]() and
and
![]() .5 Let
.5 Let
![]() be the number of elements
(measure) of
be the number of elements
(measure) of
![]() . Would
. Would
![]() everywhere inside region
everywhere inside region ![]() then
then
![]() , where
, where ![]() and
and ![]() are uniquely determined by the initial data and the geometry.
If
are uniquely determined by the initial data and the geometry.
If ![]() and
and ![]() in region
in region ![]() then
then
![]() where
where ![]() is uniquely determined by the initial data. If so, then any
observed non-zero dispersion of
is uniquely determined by the initial data. If so, then any
observed non-zero dispersion of ![]() implies degeneracy of
implies degeneracy of ![]() in region
in region ![]() and reflects curvature effects in this region. Can some statistical
effects that are normally attributed to quantum fluctuations be accounted
for through the above mechanism?
and reflects curvature effects in this region. Can some statistical
effects that are normally attributed to quantum fluctuations be accounted
for through the above mechanism?
The picture shown in Fig. 1 can be misleading in two ways. First, the
time of emerging of the probe from region ![]() is random. Second, a path of the particle should be continuous
but need not be differentiable.
is random. Second, a path of the particle should be continuous
but need not be differentiable.
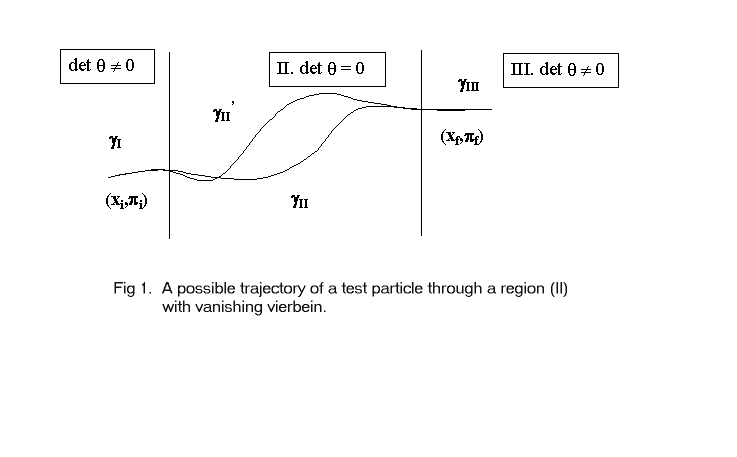
Fig. 2 shows a possible world line of a particle meeting on its way a
"bubble of vanishing vierbein" in otherwise flat Minkowski space.
Acknowledgements
Thanks are due to H.J. Borchers, H. Goenner, F. Müller-Hoisen and
H. Reeh for discussion
Bibliography
-
- 1
- A. J, Hanson and T. Regge: Torsion and quantum gravity,
Proc. Integrative Conf. on Group Theory and Mathematical Physics, University
of Texas at Austin (1978), Lecture Notes in Physics, 94, Springer-Verlag,
Berlin-Heidelberg-New York, 1979
- 2
- B. D'Auria and T. Regge, Nucl. Phys. B195 (1982),
308-324
- 3
- R. J. Petti, Gen.Rel.Grav., 7 (1976) 869-883
- 4
- K. A. Pilch, Lett. Math. Phys. 4 (1980), 49-51
- 5
- B. Giachetti, B. Piicci and E. Sorace, Lett. Math. Phys.,
5 (1981), 85-91
- 6
- J. Hennig and,E, Nitsch, Gen. Rel. Grav., 13 (1981)
947-962
- 7
- F. Müller-Hoissen and J, Nitsch, Teleparallelism - A Viable
theory of Gravity? , preprint.
- 8
- K. S. Stelle and P. C. West, Phys. Rev. D21 (1980)
1466-1488
- 9
- A. Einstein and N. Rosen, Phys. Rev. 48 (1935) 73-77
- 10
- N. Kobayashi and K. Nomizu, Foundations of Differential Geometry,
Vol. I., Interscience Pubs., New York, 1963
- 11
- W. Greub, S. Halperin, and B. Vanstone, Connections, Curvature,
and Cohomology, Vol. II., Academic Press, New York, 1972
- 12
- J. Dieudonne, Treatise on Analysis, Vol. IV, Academic Press,
New York, 1974
- 13
- A. Jadczyk, On pure gauge theories, talk at the Conf. on
Gauge Theories and Spinor Structures, University of Clausthal, July
1982
- 14
- P. C. Nelson, Phys. Lett., 79 A (1980), 285-287
- 15
- F.W. Hehl, Y. Ne'eman, J. Nitsch and P. von der Heyde, Phys.
Lett., 78 B (1978) 102-106
- 16
- E. Witten, Commun. Math. Phys., 80 (1981) 381-402;
L F Abbott and S. Deser, Nucl. Phys. B l95 (1982) 76-96;
A. Lapedes and E. Mottola, Phys. Lett. 110 B (1982)
114-116; T. Parker and C. H. Taubes, Commun. Math. Phys., 84
(1982), 223-238
- 17
- A. Jadczyk, Ann. Inst. H. Poincare, A38 (1983), 99
Footnotes
- ... GRAVITATION1
- Preprint Uni Goettingen published August 1982
- ...2
- e-mail: ajad@physik.uni-bielefeld.de
- ... theory"3
- By a pure gauge theory we mean a gauge field theory where the primitive fields have no direct connection to space-time geometry. Such a theory should "interprete itself" (see Ref. [13].
- ... possibility.4
- Another possibility is to introduce an extra pseudo-scalar field
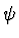 and to replace
and to replace 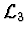 with
with
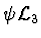 (see [14]).
(see [14]).
- ... .5
- For a non-Abelian Yang-Mills field as it is in our case a generalized flux should be used.