Algebras, Symmetries, Spaces
1
A. Jadczyk2
Inst. of Theor. Physics
University of Wroclaw
Abstract:
After discussing several aspects of noncommutative geometry from a
rather subjective point of view, algebraic techniques are shown to
offer a powerful tool for studying specific manifolds in the realm
of commutative geometry, with possible generalization to infinite
dimensions.
A possible conclusion stemming from the (till now unsuccessful)
experience with relativistic quantum field theory is that the
classical space-time model breaks down at very small distances
and it has to be replaced by some kind of a 'quantum space'. Thus,
if you 'zoom' several dozen times, you see no space and no time.
No smooth manifold structure ... only deadly noncommutative
'algebra foam'. It may seem that
noncommutative geometry is the way.
In noncommutative geometry sets are first replaced by algebras and
then forgotten. Formally: If
is a map between spaces, and if 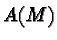 and
and 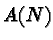 are the
respective algebras of functions on these sets, then all the
information about the map
are the
respective algebras of functions on these sets, then all the
information about the map  is, equivalently, contained in the
induced map
is, equivalently, contained in the
induced map 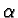 between the function algebras
between the function algebras
which is an algebra homomorphism:
Notice that the arrow has changed its direction! Thus follows the
Algorithm of noncommutative geometry:
Forget about 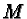 's,
's, 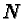 's, and
's, and  's. Reverse the arrows, and play with
's. Reverse the arrows, and play with
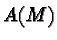 's
's 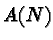 's
's 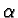 's alone, without assuming them
commutative. But: do it so as if
's alone, without assuming them
commutative. But: do it so as if 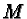 's,
's,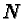 's and
's and  's existed.
's existed.
Applications of the ideas of noncommutative geometry can be found
today in several areas:
- Algebraic geometry (still Abelian)
- Super-geometry (Grassmann algebras): Berezin, Leites, Kostant,
Manin, Penkov3
- "Color" generalizations (arbitrary grading groups): Rittenberg,
Marcinek4
- Simple models: Spera, Dubois-Violette, Madore, Kerner, Connes,
quantum groups literature,
- Space-time out of an algebra: Bannier (see Ref. [5]),
Ocneanu5
One may wonder if
ALGEBRA IS THE ANSWER TO LIFE, UNIVERSE AND
EVERYTHING ?
I am not quite sure that this is indeed the case. I was lucky
enough to be given a chance of learning from Prof. Rudolph Haag,
whom you may know as one of the founders of the algebraic approach
to quantum theory. Once, when in Hamburg, I went to Prof. Haag,
all excited about a new idea concerning algebraic description of
gravity. I was surprised to hear this question: " ... yes, but
why an algebra ?" From this time on I have kept repeating this to
myself: why an algebra ? And also: why a foam ? It
was another idea discussed frequently in Hamburg (usually Detlev
Buchholz and Klaus Fredenhagen were active parties in these
discussions) that, perhaps, at an extreme zoom, at very small
distances, space-time smoothes out again, and an
"essentially free", conformally invariant field theory may be at
work at this scaling limit. It is at least interesting to
renounce, for a while, the "algebra paradigm", including its
current season's overcoat, the 'noncommutative geometry paradigm'.
When we look for alternatives, we realize that
Reversing the arrows is not what the tigers like
best.
What is then more fundamental, more primitive, than algebras? We
may think of orthomodular lattices (von Neumann, Jauch, Piron, ...
) or operational logics (Randall, Foulis, ... ). One of the
important conclusions that one can arrive at, while analyzing
foundations of quantum theory using these techniques, is
that6
quantization is the result of restriction on the set of available
states.
Thus:
States are more primitive than algebras.
Notice that if
is an algebra homomorphism, then
the induced map between states, goes the reverse way. Thus:
arrows get back their original directions.7 The generalization from
"classical" to "quantum" is now encoded in the convex geometry of
the space of states: the set of states is not necessarily a
simplex and the knowledge of pure states does not longer
suffice.8 Thus: mixed
states become important9,10, and one finds that it is
necessary to study convex and differential geometry of state
spaces11, including the study of manifolds embedded
there12. According to this Philosophy algebras
should be invoked only when they arise as duals of state
spaces.13 Till now no really
satisfactory alternative model based on this principle has been
constructed.14
Instead of replacing manifolds by algebras, we will consider here
manifolds embedded in algebras and studied by algebra
techniques.
WHY ILLUSTRATIVE ?
- bundle of C*-algebras
- Kähler manifolds naturally embedded into projective Hilbert space of quantum states
- for p=q=2 conformal symplectic manifolds
- give rise automatically to a kind of noncommutative geometry... (reserved for future applications)
References to this Section: See
[15,16,17,18,19,20]
Introduce the following notation:
More precisely, 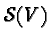 is defined as follows:
is defined as follows:
Notice that each
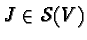 defines a
defines a 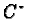 -algebra conjugation
-algebra conjugation
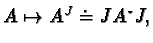 which is
the adjoint with respect to the scalar product
which is
the adjoint with respect to the scalar product 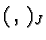 :
:
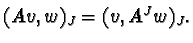
The manifold 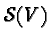 will be the subject of our study. It
carries the following remarkable predicates:
will be the subject of our study. It
carries the following remarkable predicates:
- HOMOGENEOUS
- IRREDUCIBLE
- HERMITIAN
- SYMMETRIC 15
- COMPLEX
- KÄHLER
- EINSTEIN
- NONCOMPACT
- BOUNDED DOMAIN
It is our aim here to take advantage of the fact that 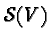 is realized as a particular submanifold in the algebra
is realized as a particular submanifold in the algebra
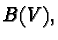 and thus allows study by algebraic techniques. In
particular we shall study:
and thus allows study by algebraic techniques. In
particular we shall study:
- Riemannian (i.e. positive definite) metric
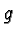 on
on 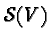
- fundamental form
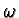
- almost complex structure
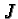
- geodesic transport
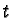
- boundary projection
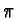
If
 has signature
has signature
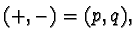
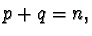 then to each
then to each 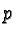 -dimensional
-dimensional 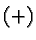 -subspace
-subspace
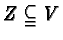 one associates the operator
one associates the operator
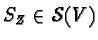 :
:
where 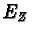 is the orthogonal projection16 onto
is the orthogonal projection16 onto 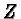 . Conversely, for each
. Conversely, for each
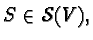 the range (= co-kernel) subspace of
the projection
the range (= co-kernel) subspace of
the projection
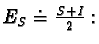
is maximal (i.e. 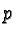 -dimensional) positive.
-dimensional) positive.
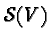 is a homogeneous space for the unitary group
is a homogeneous space for the unitary group
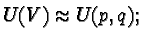 the natural action can be also described by
the natural action can be also described by
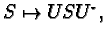 with the isotropy group
with the isotropy group
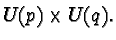 Since the central circle group of
Since the central circle group of 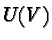 acts trivially on
acts trivially on
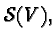 we get the isomorphism
we get the isomorphism
Notice that the denominator is the maximal compact subgroup of the
numerator.
First of all, the relations
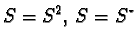 allow us to
identify the space
allow us to
identify the space
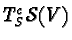 of complex tangent vectors
at
of complex tangent vectors
at
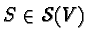 with operators
with operators 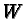 such that
such that 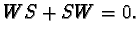 Real tangent vectors (
Real tangent vectors (
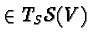 )are characterized by
the extra condition
)are characterized by
the extra condition 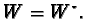 The Lie algebra
The Lie algebra
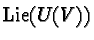 can be identified with anti-Hermitian
operators
can be identified with anti-Hermitian
operators 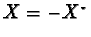 on
on 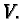 They induce fundamental (real)
vector fields on
They induce fundamental (real)
vector fields on 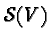 :
:
A Kählerian metric 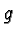 on
on 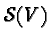 is simply
given by17
is simply
given by17
With this metric 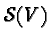 becomes a symmetric space: each
becomes a symmetric space: each
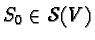 is at
the same time in
is at
the same time in 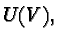 and defines the map
and defines the map
which is a geodesic symmetry at 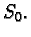
A natural almost complex structure 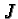 on
on 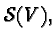
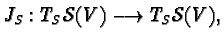 is given by
is given by
Check that 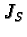 maps
maps 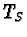 into itself:
into itself:
if 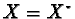 and
and 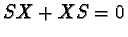 then
then
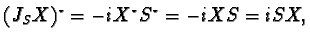
Check that 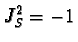 :
:
We also have
The field 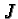 is parallel:
is parallel:
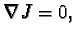 thus
thus 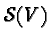 is Kählerian.
The symplectic form
is Kählerian.
The symplectic form 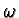 is
is
for 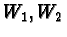 tangent at
tangent at 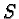 to
to 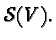 Both
Both 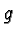 and
and
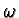 are evidently invariant under the action of
are evidently invariant under the action of 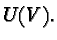 The
symplectic form is closed
The
symplectic form is closed 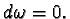
For a symplectic manifold
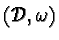 with a symplectic
action of a Lie group
with a symplectic
action of a Lie group 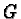 one defines the momentum mapping
(Poincaré-Cartan form) as a function
one defines the momentum mapping
(Poincaré-Cartan form) as a function
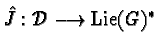 satisfying the condition
satisfying the condition
for all
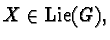 where for all
where for all
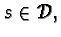 the
function
the
function 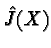 is defined by
is defined by
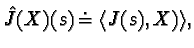 and
and 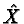 is the fundamental vector field
associated to
is the fundamental vector field
associated to 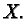 An explicit knowledge of the momentum mapping
is quite useful for a physical interpretation of the geometrical
quantities. We can easily compute the momentum map by using the
introduced algebraic technique. In our case the momentum mapping
is given by a simple formula
An explicit knowledge of the momentum mapping
is quite useful for a physical interpretation of the geometrical
quantities. We can easily compute the momentum map by using the
introduced algebraic technique. In our case the momentum mapping
is given by a simple formula
where 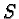 is in
is in 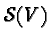 and
and 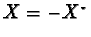 is in
is in
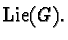
To see that the almost complex structure 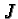 is covariantly
constant under the Levi-Civita connection of
is covariantly
constant under the Levi-Civita connection of 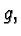 it is again
convenient to use the algebraic machine that provides an easy tool
for describing the geodesic parallel transport on
it is again
convenient to use the algebraic machine that provides an easy tool
for describing the geodesic parallel transport on 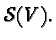 Given two points
Given two points
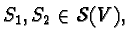 the operator
the operator 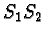 is positive with respect to the p.d. scalar products
is positive with respect to the p.d. scalar products
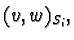
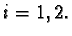 The operator
The operator
is then unambiguously defined, positive
for both scalar products, and an isometry of 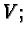 we have
we have
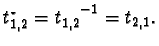 Moreover,
Moreover,
and 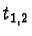 maps the
maps the 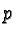 -plane
-plane 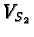 onto
onto 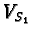 . The
most interesting property of
. The
most interesting property of 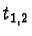 is that when applied to
tangent vectors to
is that when applied to
tangent vectors to 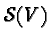 at
at 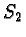 it maps them into the
tangent vectors at
it maps them into the
tangent vectors at 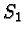 obtained by parallel transport along the
unique geodesic connecting the two points. To see this one uses
the fact that geodesics on
obtained by parallel transport along the
unique geodesic connecting the two points. To see this one uses
the fact that geodesics on 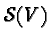 are trajectories of
one-parameter subgroups of
are trajectories of
one-parameter subgroups of 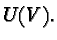 The transport operators
The transport operators 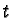 preserve the almost complex structure
preserve the almost complex structure 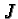 on
on 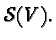 Assume
Assume 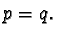 The Shilov boundary
The Shilov boundary 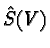 of
of 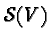 is defined as the minimal set on which bounded holomorphic
functions attain their maximum. It consists here of
isotropic
is defined as the minimal set on which bounded holomorphic
functions attain their maximum. It consists here of
isotropic 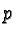 -planes. Let us fix one such plane denoted
-planes. Let us fix one such plane denoted
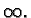 Each
Each 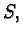 being in particular a symmetry in
being in particular a symmetry in 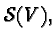 reflects
reflects 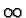 onto another isotropic
onto another isotropic 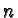 -plane
-plane
The map 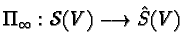 is equivariant with
respect to the stability group at
is equivariant with
respect to the stability group at  If now an origin
If now an origin  is fixed in
is fixed in 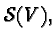 its image under
its image under 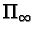 is called the antipode of
is called the antipode of 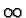 or the origin
or the origin 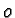 of
of 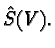 The Shilov boundary
The Shilov boundary 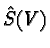 carries a natural (flat) Lorentzian conformal structure.
It is a homogeneous space not only for
carries a natural (flat) Lorentzian conformal structure.
It is a homogeneous space not only for 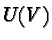 but also for the stability group of each point
but also for the stability group of each point 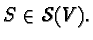

Each point 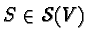 determines a Hilbert space scalar product
determines a Hilbert space scalar product
to which there correspond the "star":
In this way we produce a bundle of 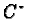 -algebras over
-algebras over 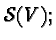 the fiber over
the fiber over 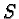 consists of the algebra
consists of the algebra 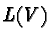 endowed
with the "star" conjugation
endowed
with the "star" conjugation 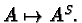 One should notice that
the fibers identify here as algebras accidentally owing to the
homogeneity of the geometry.
One should notice that
the fibers identify here as algebras accidentally owing to the
homogeneity of the geometry.
- 1
- A. Jadczyk and D. Kastler, " Lie-cartan pairs
I," Rep. Math. Phys, 25 1-51, (1987)
- 2
- A. Jadczyk and D. Kastler, "Lie-cartan pairs II,"
Ann. Phys, 179 (1987) 169-200
- 3
- R. Coquereaux, A.
Jadczyk, and D. Kastler, "Differential and integral geometry of
grassmann algebras", Rev. Math. Phys. 3, (1991)
63-100
- 4
-
W. Marcinek, "Generalized Lie Algebras I,II," Rep. Math.
Phys, (1988)
- 5
- U. Bannier, "Allgemeine kovariante algebraische
Quantenfeldtheorie und Rekonstruktion von Raum-Zeit,", PhD
thesis, University Hamburg, 1987.
- 6
-
H.D. Doebner and W. Lücke, "Quantum logic as a consequence of
realistic measurements on deterministic systems," J. Math.
Phys.
- 7
- B. Mielnik, "Theory of filters," Commun.math.
Phys, 15 (1969) 1-46
- 8
- , Ph. Blanchard and A. Jadczyk, "Event Enhanced
Quantum Theory and Piecewise Deterministic Dynamics", Ann.
der Phys 4 (1995), 583-599
- 9
- H. Araki, "On a characterization of the state space of quantum
mechanics," Commun.math. Phys, 75 (1980) 1-24
- 10
- C. Piron, "New quantum mechanics," In Essays in Honour of W.
Yourgrau, Plenum N.Y., 1983, pp. 345-361
- 11
- N. Giovannini, "Classical
and quantal systems of imprimitivity", J. Math. Phys.,
22 (1981) 2389-2403
- 12
- F. Reusse, "On classical and quantum relativistic
dynamics", Found. Phys., 9 (1979) 865-882
- 13
- B. Mielnik,
"Generalized quantum mechanics", Commun. math. Phys.,
37 (1974) 221-256
- 14
- R. Haag and U. Bannier, "Comments on Mielnik's
generalized (non linear) quantum mechanics", Commuun. math.
Phys. 60 (1975) 1-6
- 15
- A. Odzijewicz, "On reproducing kernels
and quantization of states", Commun. math. Phys., 114
(1988) 577-597
- 16
- I.T. Todorov, Conformal Description of Spinning
Particles, Springer Verlag, Berlin-Heidelberg, 1986
- 17
- G.J.
Zuckerman, "Quantum physics and semisimple symmetric spaces", in
Lect. Notes Math., 1077, 1984
- 18
- A. Jadczyk, "Geometry of
indefinite metric spaces", Rep. Math. Phys, 1 (1971)
263-276
- 19
- R. Coquereanx, "Noncommutative geometry and theoretical
physics", J. Geom. Phys 6 (1989) 425-490
- 20
- R. Coquereanx and A. Jadczyk, "Conformal
theories, curved phase spaces, relativistic wavelets and the
geometry of complex domains", Rev. Math. Phys. 2
(1990) 1-44
Footnotes
- ... Spaces1
- Talk given at the
8th International Workshop on Mathematical Physics, held at the
Arnold Sommerfeld Institute, Clausthal (Germany), July 19-26,
1989. Published in Quantum Groups, H.-D. Doebner and J.-D.
Hennig (Eds), Springer-Verlag, Berlin 1990 ( Lecture Notes in
Physics, Vol. 370, pp. 426-434)
- ...A. Jadczyk2
- e-mail: ajad@ift.uni.wroc.pl
- ... Penkov3
- See also Ref.
[1,2,3]
- ...
Marcinek4
- See [4] and references there
- ...
Ocneanu5
- Private communication
- ...
that6
- See e.g. [6]
- ... directions.7
- Which agrees
with "the natural order of things."
- ...
suffice.8
- See e.g. Ref.[7]
- ... important9
- Anyway they are important for
OPEN systems; and quantum theory of open systems may even become a
necessity if one wants to incorporate equivalence
principle.
- ...,10
- Note added on February 17, 2001: this paper
was written in July 1989. A year later the "Quantum Future"
project began, which resulted in EEQT, "Event Enhanced Quantum
Theory"
[8] , where it was shown that for quantum theory to
describe time series of events, open system
algorithms must necessarily be used
- ...
spaces 11
- in particular the most interesting infinite-
dimensional case.
- ...
there12
- E.g. Phase space can be considered in some cases as
a submanifold of the state space, the embedding being implemented
via coherent states.
- ...
spaces.13
- See e.g. Ref.[9]
- ...
constructed.14
- Notice however the discussion in Piron,
Giovannini, Reusse
[10,11,12], and also the discussion of
probabilistic interpretation of the nonlinear Schrödinger
equation: Ref. [13,14]
- ... SYMMETRIC15
- We choose the letter
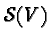 to remind the fact that
to remind the fact that 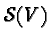 is isomorphic to the set of all geodesic symmetries of
is isomorphic to the set of all geodesic symmetries of 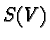 .
.
- ... projection16
- 'Orthogonal'
with respect to each one of the two relevant scalar products: the
indefinite, and the Hilbert space one obtained by flipping the
sign of the complementary subspace
- ... by17
- The methods apply as well to infinite
dimensions, but in infinite dimensions one has to take a special
care about existence of trace
's,
's, and
's. Reverse the arrows, and play with
's
's
's alone, without assuming them commutative. But: do it so as if
's,
's and
's existed.

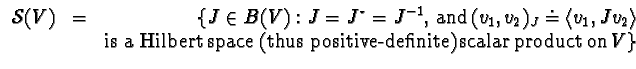
![]() will be the subject of our study. It
carries the following remarkable predicates:
will be the subject of our study. It
carries the following remarkable predicates:
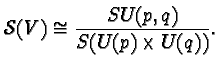
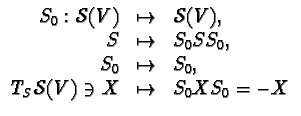
![]() and
and ![]() then
then
![]()
![]() with a symplectic
action of a Lie group
with a symplectic
action of a Lie group ![]() one defines the momentum mapping
(Poincaré-Cartan form) as a function
one defines the momentum mapping
(Poincaré-Cartan form) as a function
![]() satisfying the condition
satisfying the condition
![]() is covariantly
constant under the Levi-Civita connection of
is covariantly
constant under the Levi-Civita connection of ![]() it is again
convenient to use the algebraic machine that provides an easy tool
for describing the geodesic parallel transport on
it is again
convenient to use the algebraic machine that provides an easy tool
for describing the geodesic parallel transport on ![]() Given two points
Given two points
![]() the operator
the operator ![]() is positive with respect to the p.d. scalar products
is positive with respect to the p.d. scalar products
![]()
![]() The operator
The operator
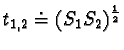
![]() is equivariant with
respect to the stability group at
is equivariant with
respect to the stability group at ![]() If now an origin
If now an origin ![]() is fixed in
is fixed in ![]() its image under
its image under ![]() is called the antipode of
is called the antipode of ![]() or the origin
or the origin ![]() of
of ![]() The Shilov boundary
The Shilov boundary ![]() carries a natural (flat) Lorentzian conformal structure.
It is a homogeneous space not only for
carries a natural (flat) Lorentzian conformal structure.
It is a homogeneous space not only for ![]() but also for the stability group of each point
but also for the stability group of each point ![]()

![]() determines a Hilbert space scalar product
determines a Hilbert space scalar product