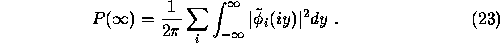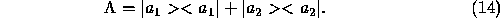


We consider now the simplest case of a composite detector. It will be an incoherent composition of two simple ones. Thus we will take:
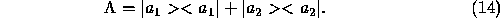
Remark Notice that if 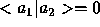 , then coherent and incoherent
compositions are indistinguishable, as in this case, with
, then coherent and incoherent
compositions are indistinguishable, as in this case, with 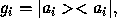 we have that
we have that 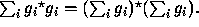
For 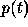 we have now the formula:
we have now the formula:
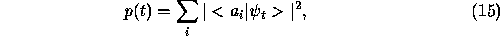
and to compute the complex amplitudes 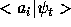 we
will use the Laplace transform method as in the case of one detector.
To this end one applies
we
will use the Laplace transform method as in the case of one detector.
To this end one applies 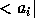 from the left and
from the left and  from the right to Eq. (11) and solves the resulting system
of two linear equations to obtain:
from the right to Eq. (11) and solves the resulting system
of two linear equations to obtain:
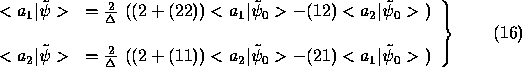
where we used the notation
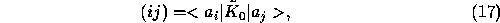
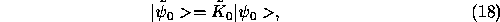
and where 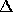 stands for
stands for
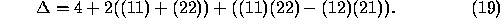
The probability density 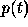 is then given by
is then given by
where 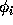 is the inverse Fourier transform
is the inverse Fourier transform
of
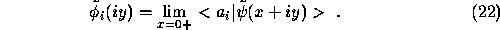
By the Parseval formula we have
that 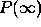 is given by:
is given by: