

Next: The Time of
Up: Time of Events
Previous: Third Postulate -
The above postulates are more or less "natural". They are in agreement
with the existing ideas of non-unitary evolution. So, for
instance, in [20] the authors considered the ionization
model. They wrote: According to the usual procedure the
ionization probability
evolution. So, for
instance, in [20] the authors considered the ionization
model. They wrote: According to the usual procedure the
ionization probability  should be given by
should be given by
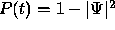 .
.
Even if our postulates are
natural, it is worthwhile to notice that EEQT allows
us to interpret them, to understand them and to derive them, in terms of
classical Markov processes.
First of all let us see that the above formula for  can be understood
in terms of an inhomogeneous Poisson decision process as follows.
can be understood
in terms of an inhomogeneous Poisson decision process as follows. Assume
the evolution starts with some quantum state
Assume
the evolution starts with some quantum state 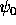 , of norm one, as
above. Define the positive function
, of norm one, as
above. Define the positive function 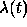 as
as
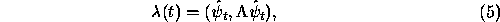
where
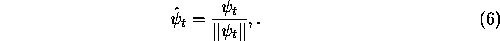
Then 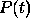 above happens to be nothing but the first-jump probability
of the inhomogeneous Poisson process with intensity
above happens to be nothing but the first-jump probability
of the inhomogeneous Poisson process with intensity  .
It is instructive to see that this is indeed the case. To this
end let us divide the interval
.
It is instructive to see that this is indeed the case. To this
end let us divide the interval 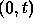 into n subintervals
of length
into n subintervals
of length 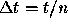 . Denote
. Denote 
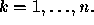 The inhomogeneous Poisson process of intensity
The inhomogeneous Poisson process of intensity 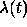 consists then of
taking independent decisions jump--or--not--jump\
in each time subinterval.
The probability for jumping in the k-th subinterval is assumed to be
consists then of
taking independent decisions jump--or--not--jump\
in each time subinterval.
The probability for jumping in the k-th subinterval is assumed to be
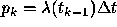 (that is why
(that is why  is called the
intensity\
of the process).
Thus the probability
is called the
intensity\
of the process).
Thus the probability 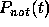 of not jumping up to time t is
of not jumping up to time t is
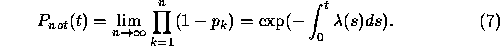
Let us show that 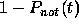 can be identified with
can be identified with 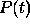 given by Eq.
(7).
To this end notice that
given by Eq.
(7).
To this end notice that
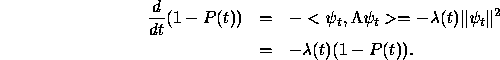
Thus 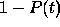 , given by Eq. (1) satisfies the same differential
equation as
, given by Eq. (1) satisfies the same differential
equation as
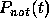 given by Eq. (7). Because
given by Eq. (7). Because 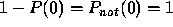 , it
follows that
, it
follows that 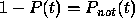 , and so
, and so 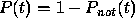 indeed is the first
jump
probability of the inhomogeneous Poisson process with intensity
indeed is the first
jump
probability of the inhomogeneous Poisson process with intensity 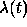 .
.
This observation is useful but rather trivial. It can not yet stand
for a justification of the formula (1) - this for the simple
reason that the jump process above, based upon a continuous observation
of the variable 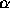 and registering the time instant of its jump, is not
a Markovian process. It would become
Markovian if we know
and registering the time instant of its jump, is not
a Markovian process. It would become
Markovian if we know  , but to know
, but to know  we must
know
we must
know 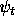 . This leads us to consider pairs
. This leads us to consider pairs 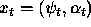 ,
where
,
where
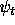 is the Hilbert space vector describing quantum state, and
is the Hilbert space vector describing quantum state, and 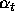 is the yes-no state of the counter. Then
is the yes-no state of the counter. Then 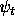 evolves deterministically
according to the formula (2), the intensity function
evolves deterministically
according to the formula (2), the intensity function 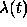 is computed on the spot, and the Poisson decision process described above
is responsible for the jump of value of
is computed on the spot, and the Poisson decision process described above
is responsible for the jump of value of 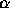 - in our case
it corresponds to a "click" of the counter. The time of the click is a
random variable
- in our case
it corresponds to a "click" of the counter. The time of the click is a
random variable 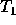 , well defined and computable by the above prescription.
, well defined and computable by the above prescription.
This prescription sheds some light onto the meaning of the quantum state vector 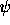 .
We see that
.
We see that 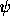 codes in itself information that is being used by
a decision mechanism working in an entirely classical way - the
only randomness we need is that of a biased (by
codes in itself information that is being used by
a decision mechanism working in an entirely classical way - the
only randomness we need is that of a biased (by 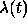 )
classical roulette. Until we ask why the bias is determined
by this particular functional of the quantum state, until then we
do not have to invoke more esoteric concepts of quantum probability
-- whatever they mean.
But, in fact, it is possible to understand somewhat more, still in pure
classical terms. We will not need this extra knowledge in the rest
of this paper, but we think it is worthwhile to sketch here at least
the idea.
)
classical roulette. Until we ask why the bias is determined
by this particular functional of the quantum state, until then we
do not have to invoke more esoteric concepts of quantum probability
-- whatever they mean.
But, in fact, it is possible to understand somewhat more, still in pure
classical terms. We will not need this extra knowledge in the rest
of this paper, but we think it is worthwhile to sketch here at least
the idea.
In the reasoning above we were interested only in what governs the
time of the first jump, when the counter clicks. But in reality
nothing ends with this click. A photon, for instance, when detected,
is transformed into another form of energy. So, if we want to
continue our process in time, after 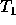 , we must feed it
with an extra information: how is the quantum state transformed
as the result of the jump. So, in general, we have a classical
variable
, we must feed it
with an extra information: how is the quantum state transformed
as the result of the jump. So, in general, we have a classical
variable 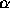 that can take finitely many, denumerably many,
a continuum, or more, possible values, and to each ordered pair
that can take finitely many, denumerably many,
a continuum, or more, possible values, and to each ordered pair
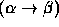 there corresponds an operator
there corresponds an operator
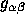 . The transition
. The transition 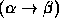 is called an event, and to each event there corresponds
a transformation of the quantum state
is called an event, and to each event there corresponds
a transformation of the quantum state
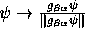 .
In the case of a counter there is only one
.
In the case of a counter there is only one 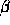 . In general, when
there are several
. In general, when
there are several 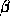 -s, we need to tell not only when to jump,
but also where to jump. One obtains in this way a piecewise deterministic
Markov process on pure states of the total system: (quantum object,
classical monitoring device). It can be then shown [6,22]
that this process, including
the jump rate formula (5) follows uniquely from the simplest
possible Liouville equation that couples the two systems.
-s, we need to tell not only when to jump,
but also where to jump. One obtains in this way a piecewise deterministic
Markov process on pure states of the total system: (quantum object,
classical monitoring device). It can be then shown [6,22]
that this process, including
the jump rate formula (5) follows uniquely from the simplest
possible Liouville equation that couples the two systems.


Next: The Time of
Up: Time of Events
Previous: Third Postulate -
Arkadiusz Jadczyk
Thu Feb 22 09:58:31 MET 1996
 evolution. So, for
instance, in [20] the authors considered the ionization
model. They wrote: According to the usual procedure the
ionization probability
evolution. So, for
instance, in [20] the authors considered the ionization
model. They wrote: According to the usual procedure the
ionization probability 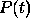 should be given by
should be given by
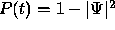 .
. can be understood
in terms of an inhomogeneous Poisson decision process as follows.
can be understood
in terms of an inhomogeneous Poisson decision process as follows. Assume
the evolution starts with some quantum state
Assume
the evolution starts with some quantum state 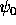 , of norm one, as
above. Define the positive function
, of norm one, as
above. Define the positive function 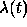 as
as


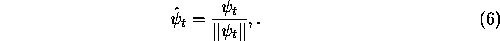
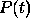 above happens to be nothing but the first-jump probability
of the inhomogeneous Poisson process with intensity
above happens to be nothing but the first-jump probability
of the inhomogeneous Poisson process with intensity  .
It is instructive to see that this is indeed the case. To this
end let us divide the interval
.
It is instructive to see that this is indeed the case. To this
end let us divide the interval 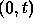 into n subintervals
of length
into n subintervals
of length 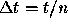 . Denote
. Denote 
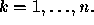 The inhomogeneous Poisson process of intensity
The inhomogeneous Poisson process of intensity 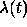 consists then of
taking independent decisions jump--or--not--jump\
in each time subinterval.
The probability for jumping in the k-th subinterval is assumed to be
consists then of
taking independent decisions jump--or--not--jump\
in each time subinterval.
The probability for jumping in the k-th subinterval is assumed to be
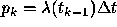 (that is why
(that is why  is called the
intensity\
of the process).
Thus the probability
is called the
intensity\
of the process).
Thus the probability 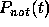 of not jumping up to time t is
of not jumping up to time t is
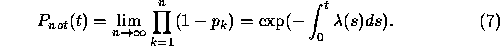
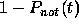 can be identified with
can be identified with 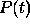 given by Eq.
(
given by Eq.
(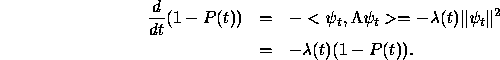
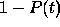 , given by Eq. (
, given by Eq. (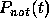 given by Eq. (
given by Eq. (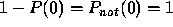 , it
follows that
, it
follows that 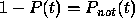 , and so
, and so 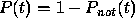 indeed is the first
jump
probability of the inhomogeneous Poisson process with intensity
indeed is the first
jump
probability of the inhomogeneous Poisson process with intensity 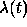 .
.
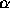 and registering the time instant of its jump, is not
a Markovian process. It would become
Markovian if we know
and registering the time instant of its jump, is not
a Markovian process. It would become
Markovian if we know  , but to know
, but to know  we must
know
we must
know 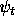 . This leads us to consider pairs
. This leads us to consider pairs 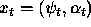 ,
where
,
where
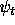 is the Hilbert space vector describing quantum state, and
is the Hilbert space vector describing quantum state, and 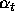 is the yes-no state of the counter. Then
is the yes-no state of the counter. Then 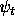 evolves deterministically
according to the formula (
evolves deterministically
according to the formula (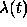 is computed on the spot, and the Poisson decision process described above
is responsible for the jump of value of
is computed on the spot, and the Poisson decision process described above
is responsible for the jump of value of 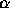 - in our case
it corresponds to a "click" of the counter. The time of the click is a
random variable
- in our case
it corresponds to a "click" of the counter. The time of the click is a
random variable 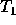 , well defined and computable by the above prescription.
, well defined and computable by the above prescription.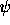 .
We see that
.
We see that 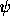 codes in itself information that is being used by
a decision mechanism working in an entirely classical way - the
only randomness we need is that of a biased (by
codes in itself information that is being used by
a decision mechanism working in an entirely classical way - the
only randomness we need is that of a biased (by 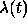 )
classical roulette. Until we ask why the bias is determined
by this particular functional of the quantum state, until then we
do not have to invoke more esoteric concepts of quantum probability
-- whatever they mean.
But, in fact, it is possible to understand somewhat more, still in pure
classical terms. We will not need this extra knowledge in the rest
of this paper, but we think it is worthwhile to sketch here at least
the idea.
)
classical roulette. Until we ask why the bias is determined
by this particular functional of the quantum state, until then we
do not have to invoke more esoteric concepts of quantum probability
-- whatever they mean.
But, in fact, it is possible to understand somewhat more, still in pure
classical terms. We will not need this extra knowledge in the rest
of this paper, but we think it is worthwhile to sketch here at least
the idea.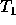 , we must feed it
with an extra information: how is the quantum state transformed
as the result of the jump. So, in general, we have a classical
variable
, we must feed it
with an extra information: how is the quantum state transformed
as the result of the jump. So, in general, we have a classical
variable 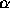 that can take finitely many, denumerably many,
a continuum, or more, possible values, and to each ordered pair
that can take finitely many, denumerably many,
a continuum, or more, possible values, and to each ordered pair
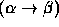 there corresponds an operator
there corresponds an operator
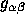 . The transition
. The transition 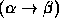 is called an event, and to each event there corresponds
a transformation of the quantum state
is called an event, and to each event there corresponds
a transformation of the quantum state
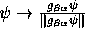 .
In the case of a counter there is only one
.
In the case of a counter there is only one 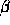 . In general, when
there are several
. In general, when
there are several 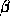 -s, we need to tell not only when to jump,
but also where to jump. One obtains in this way a piecewise deterministic
Markov process on pure states of the total system: (quantum object,
classical monitoring device). It can be then shown [
-s, we need to tell not only when to jump,
but also where to jump. One obtains in this way a piecewise deterministic
Markov process on pure states of the total system: (quantum object,
classical monitoring device). It can be then shown [